世界大百科事典（旧版）内のKellog,O.D.の言及
【関数解析学】より
…(4)の解は連続関数x(t)に連続関数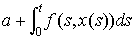
を対応させる作用素の不動点である。この考えによりG.D.バーコフとケロッグO.D.Kellog(1878‐1932)は，微分方程式の解の存在を，バナッハ空間における(必ずしも線形でない)完全連続作用素の不動点定理として証明した。このような考え方は，シャウダーJ.P.Schauder(1899‐1943)，ルレーJ.Leray(1906‐ )らによって，偏微分方程式の解の存在証明にも拡張された。…
※「Kellog,O.D.」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」