世界大百科事典（旧版）内のR左加群の言及
【加群】より
…さらに，
がベクトル，rが実数であれば，r･がベクトルになっていて，次の条件を満たしている。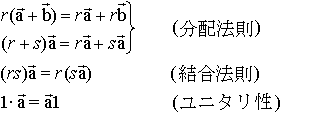 
もっと一般にMが加法に関して可換群を作っていて，Rが環であって，Rの元rとMの元mとの間の乗法が，その積rmがMの元であるように定まっていて，さらに上と同様の条件(分配法則，結合法則，ユニタリ性)が満たされているとき，MはR左加群(Rの元が左からかけられるから)という。ただし，ユニタリ性を除外して加群を定義し，ユニタリ性を満たすものをユニタリ加群と定義する立場もある。…
※「R左加群」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」