無限（読み）ムゲン（英語表記）infinity

デジタル大辞泉

む‐げん【無限】

［名・形動］《infinity》数量や程度に限度がないこと。また、そのさま。インフィニティー。「無限な（の）空間」「無限に続く」⇔有限。
[類語]永久・永遠・とわ・永世・常しえ・常しなえ・恒久・悠久・悠遠・長久・経常・不変・常磐・永劫・永代・久遠・無窮・不朽・万代不易・万世不易・万古不易・千古不易・尽きせぬ・無尽・無尽蔵・無際限・無制限・無量・無辺・底無し・底抜け・限りない・果てしない・止め処ない・エンドレス・久しい・久しぶり・久方ぶり・久久・しばらくぶり

出典　小学館

精選版 日本国語大辞典

む‐げん【無限】

1. 〘 名詞 〙
2. ① ( 形動 ) 限りのないこと。数量や程度に制限や限界のないこと。また、そのさま。無窮。無際限。
   1. [初出の実例]「七八十にして死せば長寿と云ふ可し、然ども死して以往は永劫無限也」(出典：一年有半（1901）〈中江兆民〉一)
   2. [その他の文献]〔勝鬘経‐一乗章〕
3. ② 哲学で、時間・空間の秩序の内部の部分が有限であるのに対して、先天的な時間・空間そのものをさす。形而上学で、多数の有限な現象の関係をこえて絶対的に立っているもの。神の属性の一つ。〔哲学字彙（1881）〕
4. ③ 数学で、集合Ａに対し、どのような自然数ｎをとっても、Ａと集合（1, 2, …, n）との間に一対一の対応がつかないこと。このとき、Ａの元の個数は無限であるという。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

無限 (むげん)
infinity

有限に対する概念で，一般には限りがないことを意味する。とりわけヨーロッパにおいて哲学的・数学的に主題化され，〈無限論〉として展開された。無限論は二つに大別される。すなわち可能的無限と現実的無限である。前者は無限を限りなき増大・減少と考える立場であり，不定的進行を本質とする。後者では無限は有限を超えて完結して実在する。この区別は哲学的にも数学的にも基本的である。可能的無限は古代ギリシアの無限論であり，現実的無限は近代のそれであるということができる。古代ギリシアでは無限論は哲学と数学の交錯の上に成立した。そこでは無限はアペイロンapeironと呼ばれ，文字どおり明確な限定，限界のない，形のないものである。この点からすると無限は消極的，否定的なものとならざるをえない。古代ギリシアの論理学によると，積極的に実在する無限は矛盾をもっている。かくて哲学および数学は，可能的無限において初めて無限を合理的に把捉することができた。この点でアリストテレスの哲学的無限論は典型的である。彼は《自然学》の中で次のように述べた。〈けだし無限なものというのは，それより外になにものも存在しないそれのことではなくて，かえってそれより外に常になにものかが存在するところのそれ，それが無限なものである〉。これに対して数学的無限論は尽去法（取尽くしの方法）である。この方法は現代的には無限級数の収束の証明法であるが，無限級数自体はギリシア数学では扱われていない。尽去法は求積問題において絶大な威力を発揮した。エウドクソスとアルキメデスがこれに功績がある。実際の証明は2段階を経て行われる。第1段階は，証明されるべき結果をあらかじめ獲得することである。第2段階では，その結果を否定して矛盾を導き，背理法をもって証明を完了する。この際アルキメデスの公理が必要となる。〈aとbが二つの量であって，a＜bであるとすると，na＞bとなる自然数nが存在する〉。この公理は証明の過程においては無限分割可能性を表し，可能的無限による証明を実現する。

　現実的無限が承認されるようになってきた背景には，キリスト教思想の影響が大である。例えばトマス・アクイナスは，神のみに現実的無限を認めた。神は最も完全な存在とされ，まさに無限者そのものである。そしてすべての有限を超越する。現実的無限は，この超越者の性格をもつ。中世に入ってから比較的容易に無限が論ぜられる理由はここにある。中世後期になると無限級数が自由に扱われている。現実的無限を思考するとき直ちに遭遇するのは，そのもつ矛盾である。この問題を本格的に考えた最初の人はニコラウス・クサヌスであろう。彼は神を無限なる半径をもった球になぞらえた。そしてその球ではいたるところに中心があり，周と中心が一致するという。彼は〈反対の一致coincidentia oppositorum〉を主張したことで有名である。現実的無限には，全体と部分が等しいという奇妙な性質がある。これはユークリッドの《ストイケイア》の第5公理と相いれない。したがって現実的無限を正確に思考できるためには，新しい近代の論理学が必要である。近代初期の無限論では，ブルーノ，ガリレイ，カバリエリなど多くの人をあげることができる。18世紀のカントの《純粋理性批判》の弁証論は，本質的には哲学的無限論である。そこでは無限空間，無限小，自然数全体などが自由かつ大胆に考えられている。無限小の積極的な活用に関しては，カバリエリが著名である。彼の不可分量の方法は，積分法の前身の役割を果たした。微積分学の形成は，近代初期の現実的無限の数学の頂点をなす。特にライプニッツの微積分学においてそういうことができる。ただし無限小，すなわち微分の解釈については議論が分かれ，可能的あるいは現実的とされて決着がつかなかった。

　現実的無限の数学の完成は，19世紀後半の集合論にいたってである。集合論は解析学の合理的再建を果たすとともに，無限数の理論たる超限数論への道を開いた。集合論の創始者として，デデキントとG.カントルの2人が挙げられる。カントルは自然数を拡張して超限数を定義した。超限数は，超限順序数と超限基数に分かれる。前者は0，1，2，……，n，……，ω，ω＋1，……の限りない系列をなし，後者は0，1，2，……，n，……，ℵ₀，ℵ₁，……，ℵ_ω，……の限りない系列をなす。ここで，ωは最小なる無限順序数，ℵ₀は最小なる無限基数である。この集合論では，先の現実的無限の矛盾は解決される。全体と部分が等しいことは，全体と部分が1対1対応をなすという形に変形される。これは矛盾ではない。かえってこの性質は無限集合の特性とされ，その定義に使用される（デデキント）。逆に有限集合（したがって有限）はこの性質をもたないものとして定義される。しかるに，集合論の成立後まもなく，さらに程度の高い矛盾が発見された。これが集合論のパラドックスである。多数のパラドックスの中で，ラッセルのものが最も有名かつ基本的である。それは〈自己を要素として含まない集合の絶対的全体〉を考えるとき生じる。現代の公理的集合論は，パラドックスを免れるように建設されている。そして超限数の系列の中で，極端に無限性の度合の高い数が研究できるようになった。これは巨大数の理論といわれる。
→数理哲学
執筆者：沢口 昭聿

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

無限
むげん
infinity 英語
infinité フランス語
Unendlichkeit ドイツ語

有限に対立する概念。文字どおりには限りのないことを意味する。漢語としては「無極」「無尽」「無辺」のほうが、無限の意味を伝える。哲学的な意味での無限の取扱いで注目されるのは、ギリシアにおける「アペイロン」apeironだろう。これは「ペラス」perasつまり「有限」に対立するが、それがすべての生成の源とするアナクシマンドロスの立場から、両者を生成の原理として万物が内包するものと考えるプラトンの立場まで、比較的積極的な概念として認めようとする態度と、ピタゴラス派のように数の対立概念とする立場や、それを存在するものの「外に」認めようとするアリストテレスの立場など、消極的な概念として理解する態度の双方があった。ちなみに、ギリシアでは宇宙は有限であって、空間の無限性は通常考えられていない。時間については、積極的な主張としてはかならずしも明らかではないものの、とりわけ未来に関しては開かれており、実質上無限であるとみなせる。

　キリスト教神学では、無限は単に有限の極ではなく、神に帰せられ、その意味で実体化された。われわれは神において無限を真なる存在として知ることができる。中世では、空間の有限性に関してギリシアを受け継ぎ、時間の有限性に関してはむしろその終末論的な場面で積極的に主張することになった。空間の無限性のアイデアは、神の空間性からそれを導いたニコラウス・クザーヌスに始まり、ブルーノに結晶する。この立場は汎神(はんしん)論に近づく。

　無限を数学的に扱う試みとしては、カバリエリを先駆的に、ライプニッツ、ニュートンらの微分・積分法などがあり、そこには無限小の問題も含まれている。哲学的にはカント、ヘーゲルの探求のなかに、無限は主題的に扱われるが、なんといっても、無限の技術的な定式化に目覚ましい成功を収めたのは、近代数学とくに集合論の分野であった。デーデキントは、無限を定義して次のようにいう。ある集合Mと、その真部分集合M'との間に一対一対応がつく場合に、集合Mは無限集合である。たとえば自然数の集合は、その部分集合である偶数の集合と一対一に対応するから、無限集合である。これは全体が部分に等しいことを意味しており、その意味では常識に反する。無限とは、このような常識に反するようなものとして定義されることになる。なお有限集合ではこれが成り立たない。さらに無限の程度にも区別をたてられるとされ、その「濃度」が問題にできるようになっている。

［村上陽一郎］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

無限
むげん
infinite

有限 finiteに対する語。ギリシアでは，アナクシマンドロスにより万物の根源として「無限者」ト・アペイロンが主張され，また他の哲学者たちにより一般に世界は無限に近いものであると考えられたが，中世では，キリスト教神学において神は無限であるのに対し，宇宙は有限的な，完結した世界であるとされた。しかし中世末期から近世初めにかけて，ニコラウス・グザーヌス，ブルーノらにより再び世界は時間，空間的に無限であるとされた。カントでは，純粋理性の二律背反として世界が時・空間的に無限であるか否かが問題とされたが，ヘーゲルでは，悪 (あるいは否定的) 無限と真無限とが区別された。カントルやデデキントでは，集合論の立場から有限集合，無限集合，真無限，仮無限の問題が考察された。東洋では，中国，インドなどに古くから有限，無限の思想がみられ，荘子では，わが生は有涯にして，知は無涯なりとされた。

出典　ブリタニカ国際大百科事典 小項目事典

普及版 字通

【無限】むげん

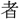限りがない。宋・契嵩(かいすう)〔読書〕詩　讀書、老いて何爲(す)るぞ　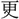に讀むも聊(いささ)か眼を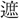(さへぎ)るのみ　此の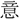、等閑と雖も　高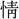、無限に寄す

字通「無」の項目を見る。

出典　平凡社「普及版 字通」

世界大百科事典（旧版）内の無限の言及

【無限大･無限小】より

…実数全体に，＋∞，－∞と書く新しい二つの要素をつけ加えて，それぞれ正の無限大，負の無限大と名付け，すべての実数aに対して－∞＜a＜＋∞なる大小関係を規約する。＋∞を単に∞と書き，無限大と呼ぶこともある。実数列｛x_n｝があって，n→∞のとき，x_n→∞となるならばx_nは(正の)無限大になるといい，x_n→－∞となるならばx_nは負の無限大になるといい，またx_n→0となるならばx_nは無限小になるという。x_nが正または負の無限大になるならば1/x_nは無限小となる。…

【数理哲学】より

…　数理哲学の課題については，古来二つの中心問題がある。一つは無限の問題であり，他は連続のそれである。無限論は無限を合理的に把握することを目ざし，無限の本性について，可能的無限と現実的無限の二つの見解に分かれる。…

※「無限」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」