アイゼンシュタインの定理（読み）あいぜんしゅたいんのていり

世界大百科事典（旧版）内のアイゼンシュタインの定理の言及

【既約】より

…また，x²＋1は実数係数の多項式としては既約であるが，複素数係数では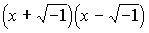と分解する。　整数係数の1変数の多項式についての既約性の判定は，一般にはむずかしいが，次のアイゼンシュタインの定理は有用である。有理整数a₀,a₁，……，a_nを係数とする多項式f(x)＝a₀xⁿ＋a₁x^n－1＋……＋a_nに対し，ある素数pがあって，(1)a₀はpで割り切れない，(2)a₁,a₂，……，a_nはpで割り切れる，(3)a_nはp²で割り切れないならばf(x)は既約である。…

※「アイゼンシュタインの定理」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」