世界大百科事典(旧版)内のコーシー=リーマンの方程式の言及
【関数論】より
…このことは,とくにf′(z0)≠0のとき,fの与える写像が局所的に等角写像となっていることと同値である。 fが複素微分可能であるためには,uとvが連続な偏導関数をもち,それらが,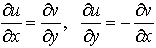 という偏微分方程式(コーシー=リーマンの方程式という)を満たさねばならない。これは必要十分条件である。…
という偏微分方程式(コーシー=リーマンの方程式という)を満たさねばならない。これは必要十分条件である。…
※「コーシー=リーマンの方程式」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
…このことは,とくにf′(z0)≠0のとき,fの与える写像が局所的に等角写像となっていることと同値である。 fが複素微分可能であるためには,uとvが連続な偏導関数をもち,それらが,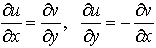 という偏微分方程式(コーシー=リーマンの方程式という)を満たさねばならない。これは必要十分条件である。…
という偏微分方程式(コーシー=リーマンの方程式という)を満たさねばならない。これは必要十分条件である。…
※「コーシー=リーマンの方程式」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...