シンプレクティック行列（読み）しんぷれくてぃっくぎょうれつ（英語表記）symplectic matrix

日本大百科全書(ニッポニカ)

シンプレクティック行列
しんぷれくてぃっくぎょうれつ
symplectic matrix

体K上の2n次列ベクトルの空間K²ⁿの交代二次形式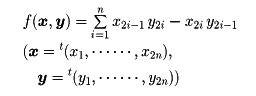

に対し、2n次正方行列Aで
　　f(Ax, Ay)＝f(x, y)　(x, y∈K²ⁿ)
を満たすAを、2n次シンプレクティック行列という。

　2n次シンプレクティック行列全体Sp(n, K)は特殊線形群SL(2n, K)の部分群になる。これをK上の2n次シンプレクティック群という。体Kが実数体R、または複素数体Cのとき、Sp(n, R)とSp(n, C)は実リー群、複素リー群になり、無限系列をつくっている4種の、いわゆる古典群の一つになっている。

［菅野恒雄］

出典　小学館　日本大百科全書(ニッポニカ)