世界大百科事典（旧版）内のディラックのδ関数の言及
【δ関数】より
…すなわち，実数xの関数δ(x)とは，x≠0のときδ(x)＝0,x＝0のときδ(0)＝∞で，
なるものとし，(－∞，∞)で連続な任意の関数φ(x)に対して，
あるいは，より一般に任意の実数cについて，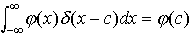
が成り立つとした。このδ(x)をディラックのδ関数，または単にδ関数と呼ぶ。このような関数は数学的にふつうの意味の関数としては認められないものであるが，1940年代後半に，フランスの数学者シュバルツL.Schwartz(1915‐ )によって創始された超関数の理論により，厳密な数学的意味づけが与えられた。…
※「ディラックのδ関数」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」
Sponserd by 