ボホナーの定理（読み）ぼほなーのていり

世界大百科事典（旧版）内のボホナーの定理の言及

【特性関数】より

…確率分布や確率変数に対して定まる一つの関数であり，初めレビP.Lévyによって導入され，確率分布の性質や確率変数列の極限などを調べるのに役だってきた。直線上の分布関数F(x)の特性関数φ(t)はスティルチェス積分，で与えられ，次の3性質をもつ。(a)tについて連続，(b)正定値，すなわちどんな有限個のt₁,t₂，……，t_nと複素数α₁，α₂，……，α_nに対しても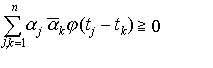(c)φ(0)＝1。逆に，(a)～(c)を満たす関数φ(t)があれば，(1)の関係にある分布関数F(x)がただ一つ定まる。…

【フーリエ解析】より

…　(－∞，∞)上の連続関数fがあって，任意の有限個の実数t₁,t₂，……，t_nと複素数α₁，α₂，……，α_nに対して，となるとき，fを正の定符号関数または正型関数という。任意の正の定符号関数fに対して，(－∞，∞)上の単調増加右連続関数σ(λ)でα(－∞)＝0なるものがただ一つ定まって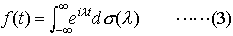，が成立する(ボホナーの定理)。逆に(3)で表される関数fは正の定符号関数である。…

※「ボホナーの定理」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」