世界大百科事典（旧版）内のポアソン積分の言及
【楕円型方程式】より
…例えばΩが平面上の単位円板の場合，その中の点を極座標(r，θ)で表し，Ωの境界(すなわち単位円周)上でのvの境界値v(1，φ)が与えられたとすると，(3)の解は，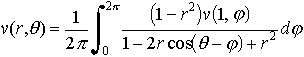
で与えられる。この右辺の積分をポアソン積分という。Ωが三次元空間の原点Oを中心とする単位球であるとき，Ωの内部の点xとΩの境界(すなわち単位球面)上の点yに対して，ベクトル
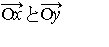とのなす角をγxyと書き，
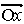の長さをrxと書くことにすると，球面上の境界値v(y)をとる(3)の解は，
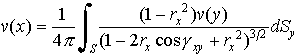で与えられる。…
【調和関数】より
…とくに，Dが原点Oを中心とする半径rの球であるとき，∂Dの連続関数fに対するディリクレ問題の解は，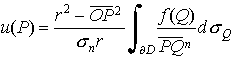
で与えられる。これをポアソン積分Poisson integralという。【及川 広太郎】。…
【ポテンシャル論】より
…この問題の解は，適当な質量を用いた積分で表すことができる。例えば，原点O中心で半径がRの球においては，その表面S上に与えられた連続な境界値をfとしたとき，ディリクレ問題の解は，次のポアソン積分によって与えられる。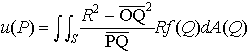
現在では，一般の空間Xの測度μとX×Xの関数K(x,y)が与えられたときに決まる関数，
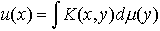のことを〈Kを核としμを質量分布とするポテンシャル〉と呼び，このような関数に関連した理論をポテンシャル論という。…
※「ポアソン積分」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」