世界大百科事典(旧版)内のラグランジュの補間公式の言及
【数値積分】より
…関数f(x)の定積分,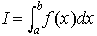 は,f(x)の不定積分F(x)がわかれば,ただちにF(b)-F(a)として求まるが,F(x)がうまく求まらないとき多項式のように定積分が容易にわかる関数p(x)でf(x)を近似して,p(x)の積分をIの近似値とする。その近似値を数値的に求めるのが数値積分である。Iをより一般に,正の値をとる重み関数w(x)をつけて,
は,f(x)の不定積分F(x)がわかれば,ただちにF(b)-F(a)として求まるが,F(x)がうまく求まらないとき多項式のように定積分が容易にわかる関数p(x)でf(x)を近似して,p(x)の積分をIの近似値とする。その近似値を数値的に求めるのが数値積分である。Iをより一般に,正の値をとる重み関数w(x)をつけて,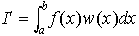 の形で扱われることが多い。I′の近似値が,
の形で扱われることが多い。I′の近似値が,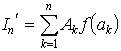 と表されるとき,akは標本点,Akは重みと呼ばれる。…
と表されるとき,akは標本点,Akは重みと呼ばれる。…
【補間法】より
…関数値が与えられている点xiのうちでxに近いn+1個の点x0,x1,……,xn(以後つねにx0<x1<……<xnとしておく)を選び,それらの点における関数値f0,f1,……,fnを用いて, f(xi)=fi (i=0,1,……,n) ……(2) という条件のもとで多項式f(x)を定めると, ここでpi(x)は次の多項式である。
ここでpi(x)は次の多項式である。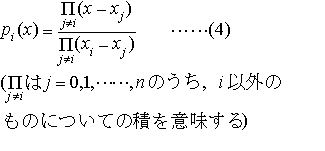 (3)をラグランジュの補間公式という。 ふつうの関数表では変数……,x0,x1,x2,……は等間隔に配置されている。…
(3)をラグランジュの補間公式という。 ふつうの関数表では変数……,x0,x1,x2,……は等間隔に配置されている。…
※「ラグランジュの補間公式」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」

