世界大百科事典（旧版）内のラドン=ニコディムの定理の言及
【積分論】より
…現代の積分論は空間の座標や位相の概念から離れて構成されるが，これはユークリッド空間におけるルベーグ積分の抽象化である。ユークリッド空間におけるルベーグ測度は面積や体積の概念の拡張であって，空集合や全空間は明らかに可測集合(ルベーグ測度が定義される集合)であり，可測集合の和，差，交わりを作る操作をたかだか可算無限回行って得られる集合は可測集合である。また可測集合Eのルベーグ測度をm(E)と書くと，どの二つも互いに交わらない可測集合の可算無限列｛En｝に対して，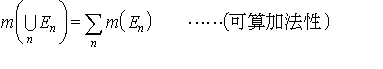
が成り立つ。…
※「ラドン=ニコディムの定理」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」
Sponserd by 