ルベーグの収束定理（読み）るべーぐのしゅうそくていり

世界大百科事典（旧版）内のルベーグの収束定理の言及

【積分論】より

…この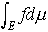が有限のときfは可積分であるという。Eで可測な関数の列｛f_n｝があって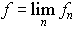，が存在し，別にEで可積分な関数gがあってE上で｜f_n(x)｜≦g(x)(n＝1,2，……)ならば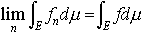，が成り立つ(ルベーグの収束定理)。　二つの空間X₁,X₂において，それぞれの部分集合のσ‐加法族B₁，B₂があり，(X₁，B₁)，(X₂，B₂)の上にそれぞれ測度μ₁,μ₂があるとする。…

※「ルベーグの収束定理」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」