双有理同値（読み）そうゆうりどうち

世界大百科事典（旧版）内の双有理同値の言及

【代数幾何学】より

…有理式R₁(x,y)，R₂(x,y)を使って，u＝R₁(x,y)，v＝R₂(x,y)によって(x,y)平面から(u,v)平面への変換(有理変換)を定めると，(x,y)平面の代数曲線f(x,y)＝0は(u,v)平面の代数曲線g(u,v)＝0に変換される。一般に二つの代数曲線f(x,y)＝0とg(u,v)＝0とが互いに有理変換できるとき，これらの曲線は双有理同値であるという。例えば直線y＝axと二次曲線u²＋v²＝1とは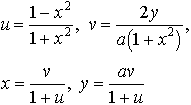，によって双有理同値である。…

※「双有理同値」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」