世界大百科事典（旧版）内の弱定常過程の言及
【確率過程】より
…
［定常過程］
確率過程｛Xt(ω)(－∞＜t＜∞)｝について，t1,t2，……，tnとhとを任意にとるとき，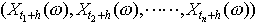
の結合分布がhに無関係であるとき，｛Xt(ω)｝を定常過程という。これに対し，平均値m(t)が定数で，共分散関数ρ(t,s)がt－sだけの関数ρ(t－s)である確率過程を弱定常過程と呼ぶ。ρ(t)はボホナーの定理により正測度μのフーリエ変換として， 
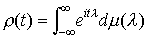と表される(スペクトル分解)。…
【定常過程】より
…dF(λ)＝f(λ)dλとかけて，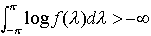
ならX(t)は移動平均表現をもち，現時点までの観測値の線形関数を用いて未来の値をよりよく推定する線形予報の問題は容易に解決される。X(t)の平均値が一定で，共分散が時間の差のみの関数であることを条件とする弱定常過程があるが，線形予報の問題は定常過程とまったく同様に扱われる。またtを連続変数にしたときの定常過程に対しても，議論は並行的に進められる。…
※「弱定常過程」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」
Sponsored by 