斉次方程式（読み）せいじほうていしき

世界大百科事典（旧版）内の斉次方程式の言及

【微分方程式】より

…b(t)≡0のとき(4)(したがって(3))は斉次，そうでないときは非斉次とよばれる。斉次方程式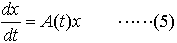，はつねに一次独立なn組の解をもち，任意の解はそれの線形結合となる。したがって一次独立なn組の解を列とする行列をΦ(t)で表せば，(5)の一般解はx＝Φ(t)c(cは定数ベクトル)，t＝t₀でx＝x⁰となる解はx＝Φ(t)Φ^－1(t₀)x⁰と表される。…

※「斉次方程式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」