世界大百科事典（旧版）内の構成可能性公理の言及
【数学基礎論】より
…L0＝｛φ｝；αが孤立数，すなわちα＝β＋1のとき，Lα＝Def(Lβ)；αが極限数のとき，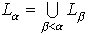
集合aがLαの要素であるとき，aを構成可能な集合と呼び，構成可能な集合の全体をLとする。VをZFの集合の全体(ユニバースと呼ばれる)とするとき，V＝Lを構成可能性公理という。ゲーデルは，⊿＝〈L，∈〉がZFのモデルをなし，しかも⊿ではV＝Lが満たされ，かつV＝LからZFの公理だけを用いて選択公理と一般連続体仮説とが導かれることを証明したのである。…
※「構成可能性公理」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」