世界大百科事典（旧版）内の正型関数の言及
【フーリエ解析】より
…また，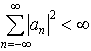
なる任意の数列｛an｝に対して，
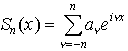はある2乗可積分な関数fに平均収束してパーセバルの等式が成立する。 (－∞，∞)上の連続関数fがあって，任意の有限個の実数t1,t2，……，tnと複素数α1，α2，……，αnに対して，
となるとき，fを正の定符号関数または正型関数という。任意の正の定符号関数fに対して，(－∞，∞)上の単調増加右連続関数σ(λ)でα(－∞)＝0なるものがただ一つ定まって，
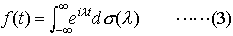が成立する(ボホナーの定理)。…
※「正型関数」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」
Sponsored by 