特有方程式（読み）とくゆうほうていしき

世界大百科事典（旧版）内の特有方程式の言及

【固有値】より

…(1)Xがn次元ベクトル空間で，XからXへの線形作用素Lが行列(a_ij)で与えられているとき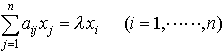，を満たすような0でないベクトル(x₁，……，x_n)が存在すれば，λはLの固有値である。それは特有方程式(または特性方程式)と呼ばれるn次方程式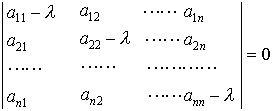，の根として与えられる。(2)Xを閉区間[a,b]上の連続関数全体のつくる線形空間，K(x，ζ)をa≦x≦b,a≦ξ≦bで連続な関数とし，XからXへの線形作用素Lを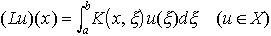，と定義する。…

※「特有方程式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」