世界大百科事典（旧版）内の《論理的推論の研究》の言及
【数学基礎論】より
…実際に，36年にゲンツェンG.Gentzenは有限の立場を一段と深化発展させることにより算術(純粋数論)の無矛盾性を達成するという画期的な仕事を行った。 ゲンツェンは1934年の学位論文《論理的推論の研究》において，数学で通常行われる推論をそのまま反映するような自然な論理計算の形式化を試み，それに技術的な推敲（すいこう）を行って1階の述語論理のまったく新しい形式の体系LK(ゲンツェン･タイプの体系という)を導入し，論理についてのまことに美しい法則〈LKで証明できる論理式は三段論法をまったく用いないで証明できる，すなわち，回り道のない証明を与えることができる〉(ゲンツェンの基本定理)を示したが，上述の36年の論文《純粋数論の無矛盾性》で，純粋数論をLKで形式化し，その無矛盾性を順序数ε0までの超限帰納法によって証明したのである。ここで，ε0とはωξ＝ξとなるような最小の順序数であって，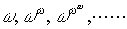
の極限数
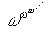である。…
※「《論理的推論の研究》」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」
Sponserd by 