世界大百科事典（旧版）内の連立常微分方程式の言及
【偏微分方程式】より
… 方程式(2)は次のようにして解ける。連立常微分方程式，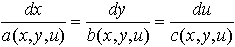
の解は一般に二つのパラメーターα,βを含む， x＝f(u；α，β)，y＝g(u；α，β) ……(3) の形に書ける。(3)はxyu空間の一つの曲線を表すので，これを(2)の特性曲線という。…
【連立方程式】より
…いくつかの方程式の組を連立方程式といい，それらの方程式すべてをみたすものをその連立方程式の解という。zの関数yについての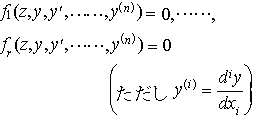
という形の方程式が連立常微分方程式で，これらすべてをみたす関数y(z)がこの連立常微分方程式の解である。yがいくつかの変数の関数であるときには偏微分が現れるが，その場合には連立偏微分方程式という。…
※「連立常微分方程式」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」