作用積分（読み）サヨウセキブン

デジタル大辞泉

さよう‐せきぶん【作用積分】

⇒作用量

出典　小学館

世界大百科事典（旧版）内の作用積分の言及

【作用量】より

…これはシュレーディンガー方程式による厳密な量子条件が確立する以前から知られていたもので，その基礎に作用変数の断熱不変性があることがP.エーレンフェストによって強調された。　上例での不定積分，すなわち運動方程式の解である軌道に沿っての積分形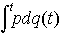，さらにもっと一般的に，ハミルトン関数Hによって記述される自由度fの系について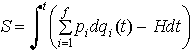，と書かれる積分は作用積分の名で呼ばれ，解析力学の定式化の中枢に位置する概念である。なぜなら，ハミルトンの原理などの運動法則を決定する変分原理は，すべてこの積分形にかかわっているからである。…

【ラグランジュ関数】より

…実際オイラーの方程式(1′)は座標の選び方によらぬ形式である(これに対しLを用いない運動方程式を直接変数変換しようとすると，多くの場合非常に複雑となる)。　さて，解析力学に現れる上述のラグランジュ関数の場合，積分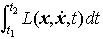は作用積分の名で呼ばれ，運動方程式の解である軌道に沿っての積分ならば，積分結果は作用S(x(t)，t)の両端値の差S(x(t₂)，t₂)－S(x(t₁)，t₁)に等しい。20世紀に至って量子力学が誕生し，波動関数とこの作用積分との関係が永く論ぜられているが，1948年R.P.ファインマンは経路積分を導入して波動関数を古典力学の軌道群によって表現することを提案した。…

※「作用積分」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」