作用量（読み）サヨウリョウ（その他表記）action

デジタル大辞泉

さよう‐りょう〔‐リヤウ〕【作用量】

エネルギーと時間、または運動量と長さの積と同じ次元をもつ物理量。変分原理で定義される積分量であり、任意の座標変換に対し、不変量となる。作用積分。

出典　小学館

改訂新版　世界大百科事典

作用量 (さようりょう)
action

ある物理量がエネルギー×時間，または運動量×座標（長さ）の次元をもつとき，この物理量は作用の次元をもつといい，そのような量を広い意味で作用量と呼ぶ。古典力学，または解析力学においては，作用量は歴史的にみても，また理論の構成のうえからも重要な意味をもつ基本量である。

　一自由度の力学系の軌道が，一般化座標qとそれに対する正準運動量pの直交座標空間（相空間といい，今の場合平面，すなわち相平面）において，一つの閉曲線を描くとき，この閉曲線（閉軌道と呼ぶ）内部の面積は一つの典型的な作用量である。この例は，力学系が外部との間に熱的なエネルギーのやりとりなしでゆっくり変化を受ける場合，軌道が変形しても閉軌道内部の面積は不変に保たれるという断熱不変性の理由で重要である。実際，この断熱不変量としての内部面積が，ある普遍定数h（プランク定数）の整数倍（一般には（n＋α/4）h。n＝0，1，2，……，0≦α/4＜1，αのことをマスロフの指数と呼ぶ）でなければならないという命題によって，この力学系の量子条件が提出された。定数hが作用量子という名称で呼ばれる理由でもある。前述の閉軌道の面積を閉軌道に沿う積分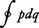で表し，これをこの力学系を記述する作用変数と呼び，ふつうJという記号で表す。Jはエネルギー積分Eの関数として求められるので，上の量子条件より系のエネルギー準位がJ（E）＝（n＋α/4）h を満たすものとして近似的に求められる。これはシュレーディンガー方程式による厳密な量子条件が確立する以前から知られていたもので，その基礎に作用変数の断熱不変性があることがP.エーレンフェストによって強調された。

　上例での不定積分，すなわち運動方程式の解である軌道に沿っての積分形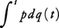，さらにもっと一般的に，ハミルトン関数Hによって記述される自由度fの系について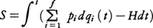，と書かれる積分は作用積分の名で呼ばれ，解析力学の定式化の中枢に位置する概念である。なぜなら，ハミルトンの原理などの運動法則を決定する変分原理は，すべてこの積分形にかかわっているからである。そして変分原理の結果として定められた，相空間における軌道に沿った積分値は，積分の両端における相空間内の座標成分q_i（i＝1，……）と時刻tだけで定まる関数となり，ハミルトン=ヤコビの偏微分方程式に従う。この偏微分方程式の一般解を求めることは系の軌道を決定することと同等である。例えば適当な正準変換により，一つの自由度が他自由度からハミルトン関数において分離される場合，これに対応して作用積分Sは分離された自由度に関する作用積分S₁と，残りの自由度に関する作用積分S′との和，すなわちS＝S₁＋S′のように表されることになる。さらにこの自由度に関し閉軌道が得られれば，その作用変数J₁と対応する共役変数w₁（作用変数に対して角変数という）とで1組の解が求められる。

　前述の古典量子条件に関連して興味ある問題に，量子力学では作用量がどのように定義され，またどのような役割を果たすかということがある。シュレーディンガー方程式に従う波動関数（三次元直交系の場合）ψ（r，t）およびその複素共役をψ^＊（r，t）とするとき（rは位置ベクトル），ρ（r，t）＝ψ^＊（r，t）・ψ（r，t）は粒子の存在確率密度を表すが，ψのいわば波としての位相因子が作用量に対応するもので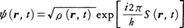，としてS（r，t）を定義すると，これはh→0の極限で古典粒子の作用積分に一致することが確かめられる。
執筆者：長谷川 洋

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

作用量
さようりょう
action

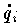一般座標 q_i ，一般速度  ，一般運動量 p_i(i＝1，2，…，n) を用いて次の積分で定義される量。
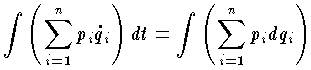作用量の変分がゼロであるという最小作用の原理は力学の基本法則を導く。作用量はエネルギーと時間との積の次元をもち，座標変換に対して不変な量である。量子論では周期運動に対する作用量はプランク定数 h の整数倍の値をもち，定数 h は作用量の単位という意味から作用量子とも呼ばれる。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

作用量【さようりょう】

広義には，エネルギー（仕事）と時間の積と同じ次元をもつ量で，座標変換により変化せず，力学の法則や変分＝０（変分学）の形で与えられるもの。狭義には，質点の運動量を運動経路に沿って積分したもの。実際の運動経路に対し，エネルギー一定の条件のもとで，この積分の値が極小になる（最小作用の原理）。→プランク定数

出典　株式会社平凡社