数学

日中辞典 第3版

数学
すうがく

数学shùxué．

ぼくは～数学が不得意だ｜我数学学得不好．

数学的帰納法

数学归纳法shùxué guīnàfǎ．

数学的論理学

符号逻辑fúhào luóji．

[関連記事]数学

1数学用語と記号

数学の用語に関しては，日本語の漢字表記と中国語の簡体字表記の違いを除けば，同じであるものが多い．以下，日本の高等学校までの範囲で出てくる用語のうち，日中で異なる主なものを掲げる．

因数分解｜因子分解yīnzǐ fēnjiě

n乗｜n次幂cì mì

n乗根｜n次根cì gēn

確率｜概率gàilǜ，几率jīlǜ

関数｜函数hánshù

1次関数｜一次函数，线性xiànxìng函数

n次関数｜n次函数

（第n階）導関数｜（n次，n级jí）导dǎo函数

逆数｜倒数dàoshù

行列｜矩阵jǔzhèn

グラフ｜图形túxíng

最大（値）｜极大（值）jí dà(zhí)

最小（値）｜极小（值）jí xiǎo(zhí)

次元（数）｜维（数）wéi(shù)

集合｜集（合）jí(hé)

差集合｜差集chājí

積集合｜积集jījí，交集jiāojí

部分集合｜子集zǐjí

補集合｜补集bǔjí，余集yújí

和集合｜和集héjí，并集bìngjí

重根｜多重根duōchónggēn

接線｜切线qiēxiàn

接点｜切点qiēdiǎn

総和｜求和qiúhé

台形｜梯形tīxíng

楕円(だえん)｜椭圆tuǒyuán

（円の）中心｜圆心yuánxīn

直方体｜长方体chángfāngtǐ

直交｜正交zhèngjiāo

展開式｜展式zhǎnshì，展开式zhǎnkāishì

複素数｜复数fùshù

分散｜方差fāngchā

ベクトル｜向量xiàngliàng

変数｜变量biànliàng

方程式｜方程fāngchéng

連立方程式｜方程组zǔ

放物線｜抛物线pāowùxiàn

補題｜引理yǐnlǐ

要素，元｜元素yuánsù

累乗｜乘方chéngfāng

数学の記号（カッコ内はその日本語の読み方）も基本的なものから選んで列挙する．

＋（足す，プラス）｜加（上）jiā(shàng)

－（引く，マイナス）｜减（去）jiǎn(qù)

±（プラスマイナス）｜正负zhèngfù

×（掛ける）｜乘（以）chéng(yǐ)

÷（割る）｜除（以）chú(yǐ)

＝（イコール，等しい）｜等于děngyú

≠（ノットイコール，等しくない）｜不等于

＜（小なり）｜小于xiǎoyú

≦（小なり（または）イコール）｜小于或等于

＞（大なり）｜大于dàyú

≧（大なり（または）イコール）｜大于或等于

≈（近い，近似）｜约yuē等于，逼近bījìn

≡（合同，同値）｜叠合diéhé，全等于

∽（相似）｜相似xiāngsì

x²（xの2乗，xの平方）｜x平方píngfāng

x³（xの3乗，xの立方）｜x立方lìfāng

xⁿ（xのn乗）｜x的n次幂

√x（xの平方根，xの2乗根）｜x的平方根

∛x（xの立方根，xの3乗根）｜x的立方根

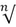x（xのn乗根）｜x的n次根

e（ネイピア数，自然対数の底）｜纳皮尔Nàpí'ěr数，自然对数的底zìrán duìshù de dǐ

logx（＝log_ex）（xの自然対数，ログx，ログイーのx）｜x的自然对数，以e为底数dǐshù的对数

log₁₀x（xの常用対数，ログ10のx）｜x的常用对数，以10为底数的对数

π（円周率）｜圆周率yuánzhōulǜ

i（虚数単位）｜虚数单位xūshù dānwèi

∞（無限大，インフィニティ）｜无限大wúxiàndà

2数学表現（基本編）

数学の基本的な表現として，四則演算，指数・対数，比較・関係についての例を挙げる．なお，文字（x，yなど）の発音は英語のそれに従うので，日中間に違いはない．

2.1 四則演算

7x＋2x＝9x｜

(ⅰ)7xプラス2xイコール9x，7xプラス2xは9xに等しい｜7x加2x等于9x

(ⅱ)7x足す2xは9x｜7x加2x得9x；7x加2x是9x

（注）以下では(ⅰ)の表現のみを記すが，(ⅱ)と同様な表現も可能．

x/2＋¾x＝5/4x（2分のxプラス4分の3xイコール4分の5x）｜2分之x加4分之3x等于4分之5x

-4y-3y＝-7y（マイナス4yマイナス3yイコールマイナス7y）｜负4y减3y等于负7y

⅔x-x/6＝x/2（3分の2xマイナス6分のxイコール2分のx）｜3分之2x减6分之x等于2分之x

2a・（-4b）＝-8ab（2a掛けるマイナス4bイコールマイナス8ab）｜2a乘负4b等于负8ab

m÷n＝m/n（m割るnイコールn分のm）｜m除以n等于n分之m

5p÷p/q＝5p・q/p＝5q（5p割るq分のpイコール5p掛けるp分のqイコール5q）｜5p除以q分之p等于5p乘p分之q等于5q

2.2 指数・対数

（3x）^-2＝1/9x²（3xのマイナス2乗イコール9x2乗分の1）｜3x的负2次幂等于9x平方分之1

xⁿyⁿ＝（xy）ⁿ（xのn乗掛けるyのn乗はxyのn乗に等しい）｜x的n次幂乘y的n次幂和xy的n次幂相等

log₁₀10^r＝r（ログ10の10^rイコールr，10^rの常用対数はr）｜10的r次幂的常用对数是r

logMN＝logM＋logN（MNの（自然）対数は，Mの対数とNの対数の和に等しい）｜MN的（自然）对数等于M的对数加N的对数

2.3 比較・関係

x²≧0（xの2乗は正またはゼロ）｜x平方大于或等于零

π≠3（πは3に等しくない，πは3ではない）｜π不等于3，π不是3

x≈±1（xは±1に近い，xは1または-1に近い）｜x约等于±1，x约等于1或-1

ABC≡PQR（三角形ABCと三角形PQRは（互いに）合同）｜三角形ABC和三角形PQR（互相）叠合

3数学表現（応用編）

数学の文章の基本構造は，仮定から結論に至る論証の流れである．そのため，数学の文章表現には，「…と仮定する，もし…ならば」“假定jiǎdìng”“假若jiǎruò”“若ruò”，「…とおく」“令lìng”，「～を…とする」“设shè～为wéi……”“设～是……”，「このとき」“则zé”，「よって，そこで，したがって」“故gù”“因此yīncǐ”“于是yúshì”，「…なので，…から」“因为yīnwei”“由yóu”“由于yoúyú”といった言葉が頻繁に使われる．また，対象の限定や結果の記述のために，「…に対して」“对（于）duì(yú)”，「…とするとき」“（当）……时(dāng)……shí”，「かつ」“且qi씓并且bìngqiě”，「または」“或huò”，といった言葉もよく用いられる．

以下，これらの言葉が使われる表現をいくつか挙げる．

1＜|x|＜2ならば，1＜x＜2または-2＜x＜-1｜若1＜|x|＜2，则1＜x＜2或-2＜x＜-1

（a-b）²はa²-2ab＋b²と展開できる｜（a-b）²可展成a²-2ab＋b²

方程式（x-a）²＋（y-b）²＝r² (1)は，中心（a，b），半径rの円を表す｜方程(1)表明biǎomíng以（a，b）为圆心yuányīn以r半径bànjìng的圆

集合A，Bが同じであるための必要十分条件は，A⊂BかつB⊂Aが成り立つことである（A＝B⇔A⊂BかつB⊂A）｜集合A，B相等的充分必要条件chōngfèn bìyào tiáojiàn是B包含bāohánA（A是B的子集）并且A包含B（B是A的子集）

4人名を冠した定理・法則など

数式による数学の表現は，ほぼ万国共通の形式になっている．そのため，日本語または中国語を母国語とする者が相手国の言葉で書かれた数学の書物を読むことは，文学作品を読むことよりやさしい．難しい点を挙げるならば，定理や法則に冠せられた人名の表記であろう．定理，補題，法則といった言葉の前に，中国語の書物では見慣れない漢字，日本語の書物ではカタカナが並んでいる場合，それは人名の音訳やカタカナ表記とみなしてまず間違いがない．文字の発音を正しく行って聞いたことのある人物名に思い当たるまでの過程は，謎解きのようなおもしろさがある．例をいくつか紹介しておく．

ピタゴラスの定理｜毕达哥拉斯定理Bìdágēlāsī dìnglǐ

下のような直角三角形ABCにおいて，（AC）²＋（BC）²＝（AB）²が成り立つ｜在如下直角三角形ABC中，（AC）²＋（BC）²＝（AB）²成立．

直角三角形ABCにおいてAC＝4，BC＝3ならば，ピタゴラスの定理からAB＝5となる｜在直角三角形ABC中若AC＝4，BC＝3，则由毕达哥拉斯定理知AB＝5

ド・モルガンの法則｜德・摩尔根（的）定律Dé-mó'ěrgēn (de) dìnglǜ

ド・モアブルの定理（cosθ＋isinθ）ⁿ＝cos（nθ）＋isin（nθ）｜德・摩弗Dé-mófó定理，穆瓦弗雷Mùwǎfóléi定理

パスカルの三角形｜帕斯卡Pàsīkǎ三角形

ユークリッドの互除法｜欧几里得Ōujīlǐdé算法

出典　中日辞典 第3版