ロンスキアン（その他表記）Wronskian

改訂新版　世界大百科事典

ロンスキアン
Wronskian

n階線形微分方程式，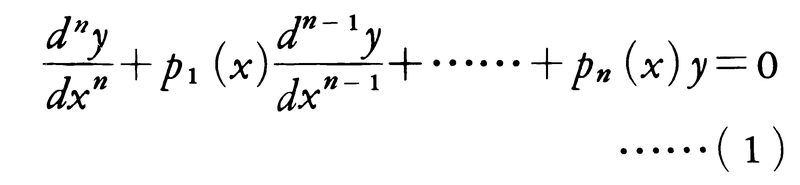

においてp₁（x），……，p_n（x）はある区間Iで連続とする。（1）のn個の解y₁（x），……，y_n（x）から作られる行列式，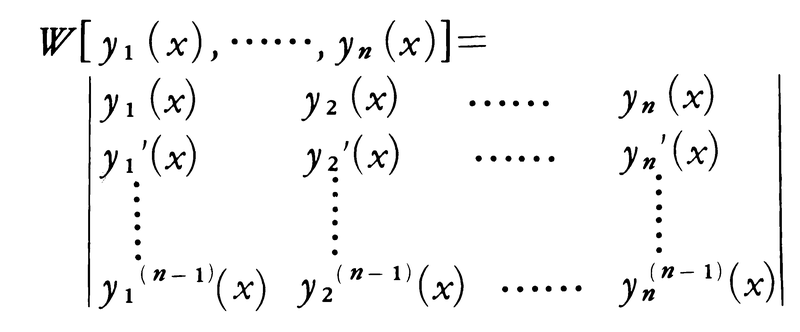

をそれらの解のロンスキアン，またはロンスキH.J.M.Wronski（1778-1853）の行列式という。これについては，Iに含まれる任意のx₀，xに対し，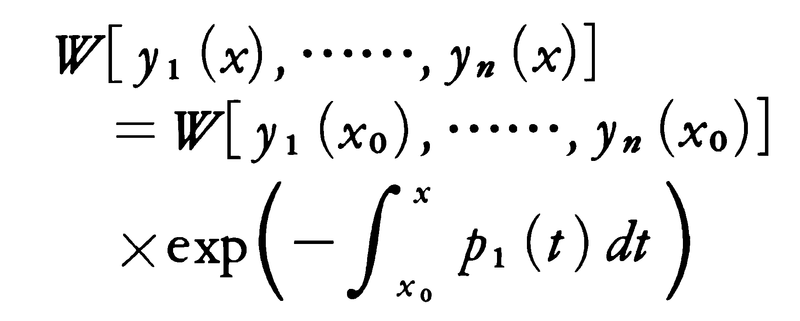

という関係が成り立つ。このことからロンスキアンがあるxに対して0となれば，じつは恒等的に0であることがわかる。W［y₁（x），……，y_n（x）］≠0であるとき，解y₁（x），……，y_n（x）は一次独立であるという。この場合には（1）の任意の解は定数c₁，……，c_nを適当に選ぶことにより，

　y＝c₁y₁（x）＋……＋c_ny_n（x）

と表すことができる。
執筆者：斎藤 利弥

出典　株式会社平凡社「改訂新版　世界大百科事典」