行列式（読み）ギョウレツシキ（その他表記）determinant

デジタル大辞泉

ぎょうれつ‐しき〔ギヤウレツ‐〕【行列式】

行列の要素が一定の規則で展開され、決まった値をもつもの。例えば、1行目の要素がa、bで、2行目の要素がc、dである2行2列の行列ではad－bcの値となる。

出典　小学館

精選版 日本国語大辞典

ぎょうれつ‐しきギャウレツ‥【行列式】

1. 〘 名詞 〙 数学で、行列に付随するある種の式または数。一定の規則に従って、行列の各行各列から要素を取り出してつくった積に正負の符号を与えたものの総和。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

行列式 (ぎょうれつしき)
determinant

行列式は連立一次方程式の解に関連して考えられたものであり，行列より歴史が古い。例えば，二元一次連立方程式，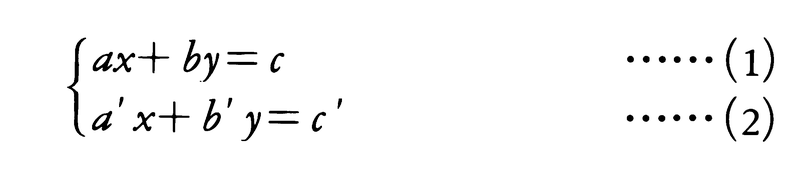

を考えると，（1）×b′－（2）×bによって，

　（ab′－a′b）x＝cb′－c′b

が得られるが，このとき，という配列から，斜めに掛算して差をとった，

　ab′－a′b，bc′－cb′

が現れている。これが二次の行列式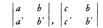，であり，ab′－a′b≠0のときの解は，

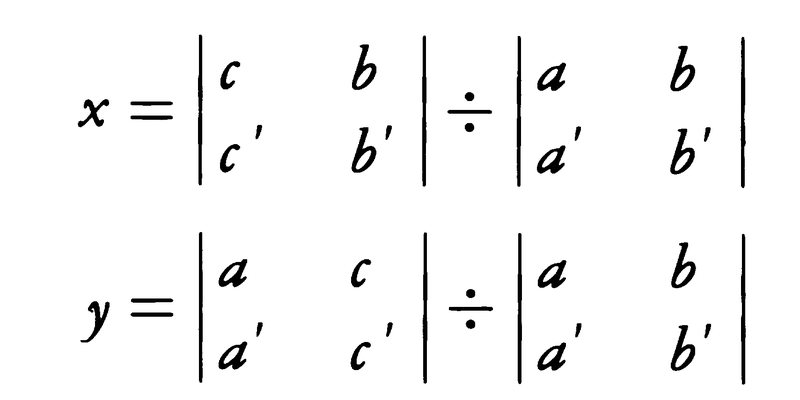
で与えられる。もっと変数の多い場合を含めて考えて，行列式が考え出された。

　和算では関孝和が1683年の著書《解伏題之法》で交式斜乗の法と称して扱ったが，三次までは正しく，四次以上は誤っていた。井関知辰は1690年の《算法発揮》で正しく扱った。名称は，二次，三次，四次，五次の行列式がそれぞれ前後平方式，前後立方式，前後三乗方式（四乗ではない），前後四乗方式であった。ヨーロッパではクラメールG.Cramer（1704-52）が創始者とされるが，その萌芽は93年のG.W.ライプニッツの書簡の中にみられる。19世紀中ごろになって，A.ケーリー，J.J.シルベスター，プリュッカーJ.Plücker（1801-68），W.R.ハミルトンらがいろいろな場面での活用を始めた。英語ではdeterminantといい，これは決定因子という意味の言葉であり，一次連立方程式の解を決めるのに重要なものということで名付けられたという。明治の日本では当初デテルミナントといったが，後にdeterminantの訳を行列式，matrixの訳を行列とするのが定着した。

定義

行列式は正方行列に対して定義され，｜A｜，det Aなどの記号が用いられる。

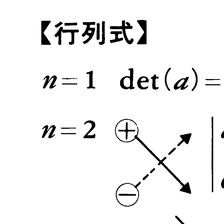
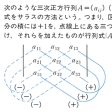
　n＝1，2，3の行列式は，図に示す定義式により，多項式に展開される。n＝4では，項の数が24あるので，n≧4のときは，一般の定義式でまとめよう。

　Aの（i，j）成分がa_ijであるとき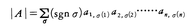，　ここに，σは｛1，2，……，n｝の上の置換n！個全部を動き，sgnσは，σが奇置換のとき－1，偶置換のとき＋1とする。

　具体的計算には，定義に従ってn！個の項を計算したのではたいへんであるので，次に述べる基本的性質，とくに（6）を利用して，計算上のくふうをすることが必要であろう。

基本的性質

（1）detA＝det（^tA）

したがって，以下列といっているところを，すべて行におきかえても正しい。

　見やすくするため，n次正方行列Aの列ベクトルをa₁，a₂，……，a_nと書き表そう。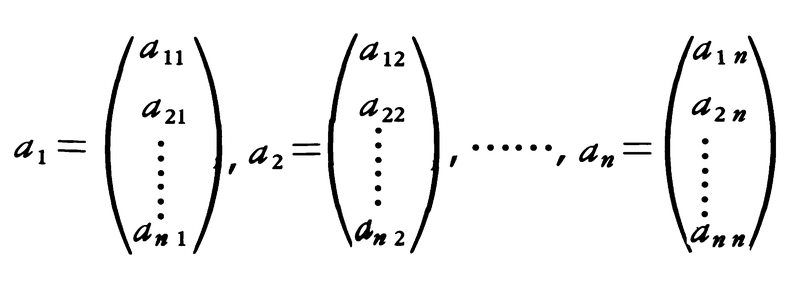

（2）一つの列をc倍したとき，

　det（a₁，……，a_α-1，ca_α，a_α+1，……，a_n）＝c・det（a₁，……，a_α-1，a_α，a_α+1，……，a_n）

とくに，ある列が0ならば，行列式は0である。

（3）一つの番号αについて，a_α＝b_α＋c_αとベクトルの和に分解したとき，

　det（a₁，a₂，……，a_α-1，b_α＋c_α，a_α+1，……，a_n）　　＝det（a₁，……，a_α-1，b_α，a_α+1，……，a_n）＋det（a₁，……，a_α-1，c_α，a_α+1，……，a_n）

（4）列の順序を置換σで変えたとき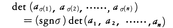，（5）二つの列が一致すれば行列式は0である。

（6）一つの列の何倍かを，他の列に加えても行列式の値は変わらない。したがって，

　det（a₁＋c₂a₂＋……＋c_na_n，a₂，……，a_n）＝det（a₁，a₂，……，a_n）

（7）n次正方行列Aに対して，そのi行およびj列を除いてできるn－1次の行列A_ijをとる。（－1）ⁱ⁺^jdetA_ij＝d_ijとおくと，

　各j＝1，2，……，nについて

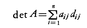　各i＝1，2，……，nについて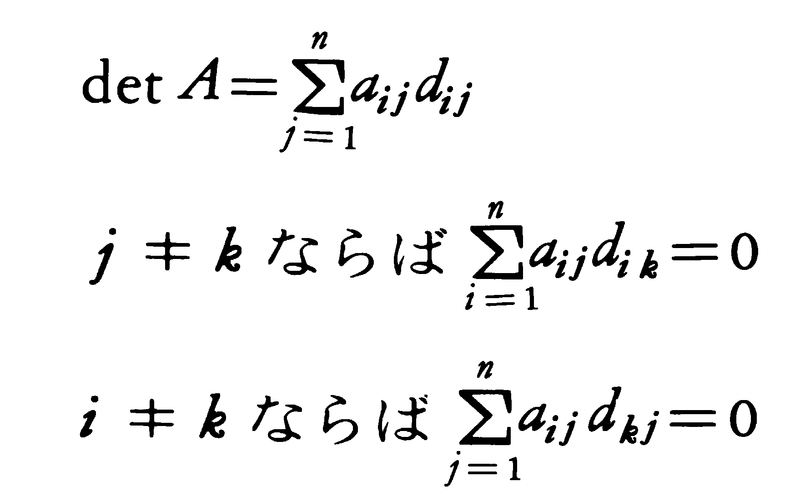

上で得た値d_ijをAの（i，j）余因子という。d_ijを（i，j）成分にもつ行列D＝（d_ij）を考えれば，上の関係はA（^tD）＝（^tD）A＝（detA）I（Iはn次の単位行列）ということと同じである。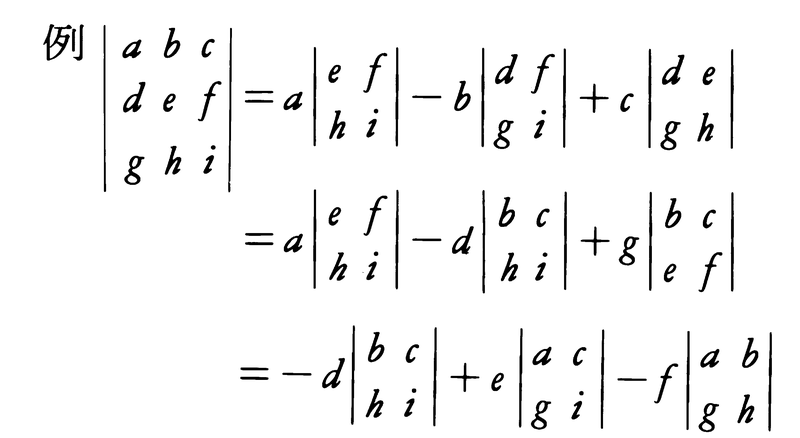

（8）A，Bがそれぞれm，n次の正方行列のとき，Oは（m，n）型の零行列として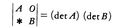，とくに，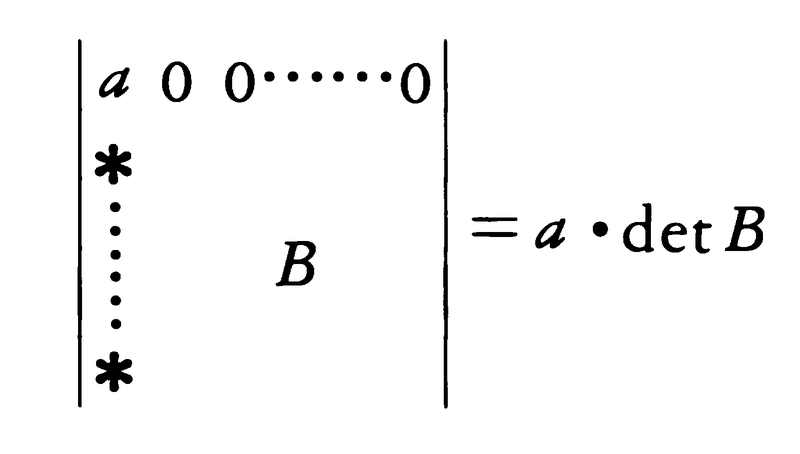

（9）A，Bがともにn次正方行列のとき，

　det（AB）＝（detA）（detB）

特殊な行列式

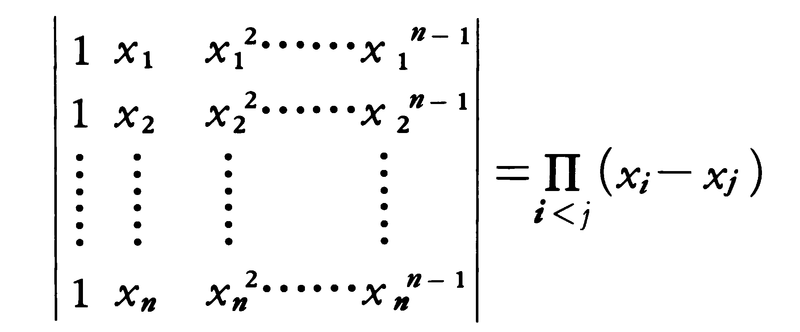
これをバンデルモンドの行列式という。

これを巡回行列式という。

一次変換と面積，体積

ユークリッド平面の一次変換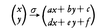，について，ある図形Fの面積がSであれば，この一次変換によるFの像σ（F）の面積は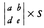の絶対値である。

　三次元ユークリッド変換，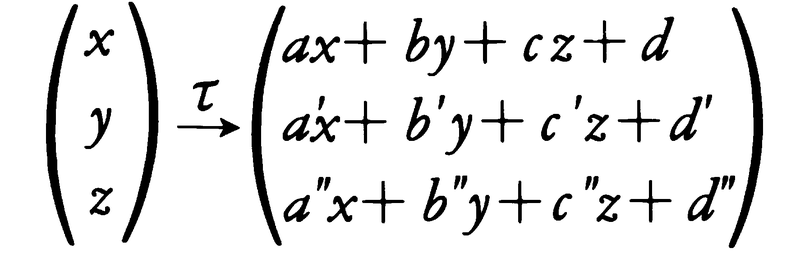

について，ある立体Cの体積がVであれば，Cのτによる像τ（C）の体積は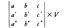，の絶対値になる。
執筆者：永田 雅宜

図－行列式

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

行列式
ぎょうれつしき
determinant

n次行列式とは、n²個の数a_ij(i, j＝1, 2,……, n)を正方形に並べた記号で表される数で、a_ijの、ある多項式の形に展開できる。n次正方行列（マトリックス）が正方形に並べられた数表であるのに対し、行列式は数であることに注意する必要がある。

　二つの未知数x、yの連立一次方程式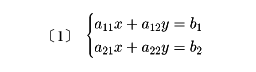

において、a₁₁a₂₂－a₂₁a₁₂≠0なら、〔1〕は消去法によって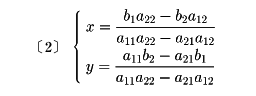

と解くことができる。〔2〕式の分母a₁₁a₂₂－a₂₁a₁₂は二次正方行列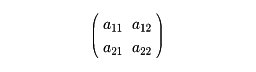

の四つの成分の多項式の形で得られる数である。いまかりに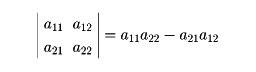

と約束すれば、x、yの分子も同様に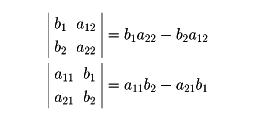

と表すことができる。このような考え方を、変数を増やしてn次正方行列の場合に推し進め、初めて行列式を一般に定義し論じたのはライプニッツやクラメルである。

［菅野恒雄］

　日本の和算家関孝和(せきたかかず)も1683年（天和3）『解伏題之法』において行列式論を展開している。伏題とは二元以上の連立方程式となる問題である。問題が複雑になれば、一つの未知数xだけでは容易に方程式がたてられない。この場合、補助の未知数y、zなどを用いていくつかの方程式をつくり、これから補助の未知数を消去して、xだけの方程式をつくる。この消去にあたって行列式が用いられるのである。この行列式を解くには、三元の場合にはいわゆるサラスの方法を用い、四元以上の場合も、これに準じた方法を用いた。しかし五元以上の解き方には誤りがあったので、後世、これは訂正されている。

［大矢真一］

行列式の定義

複素数（実数の場合を含む）a_ijを成分とするn次正方行列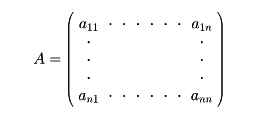

に対し、1, 2,……, nの置換σすべてにわたる和 Σsgn(σ)a_1σ(1)a_2σ(2)……a_nσ(n)を行列Aの行列式といい、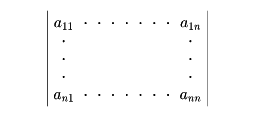

または、簡略化して、|A|またはdetAで表す。ただし、ここでsgn(σ)は置換σの符号で、σが偶置換なら＋1、奇置換なら－1をとる。a_ijを変数と考えると行列式|A|はn²個の変数の多項式で、1, 2,……, nの置換の個数のn！個の単項式の和である。n＝2のときは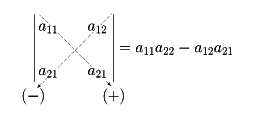

であり、n＝3のときは「サラスの方法」がある。n＝1のときは|a₁₁|＝a₁₁となるが、この左辺は絶対値と紛らわしいので、この記号は用いないことが多い。n≧4のときは行列式の計算に実際使える公式はない。後に述べる基本性質の(6)や展開公式を用いる。特殊な形の行列の行列式は定義式から簡単に出る。たとえば、一つの行または列の成分がすべて0なら、その行列式は0であり、また、たとえば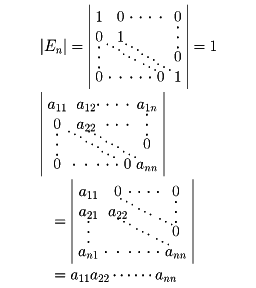

［菅野恒雄］

行列式の基本性質

行列式の定義式から次の基本性質が出る。

(1)正方行列Aの行列式とAの転置行列^tAの行列式は等しい。つまり|^tA|＝|A|である。この性質から、正方行列Aの行列式の、行について成り立つことは列についても成り立ち、また、この逆も正しい。

(2)正方行列Aの一つの行、たとえば第i行の成分a_ijが二つの数の和
　　a_ij＝a′_ij＋a″_ij (j＝1,……,n)
であれば、Aの行列式|A|は、Aの(i, j)成分を、それぞれ、a′_ij, a″_ijに置き換えた二つの行列の行列式の和に等しい。つまり

なお、列についても同様のことがいえる。

(3)正方行列Aの一つの行の成分を、c倍して得られる行列の行列式は|A|のc倍である。つまり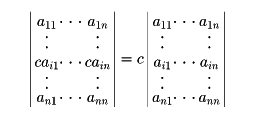

なお、列についても同様のことがいえる。

(4)正方行列Aの二つの行を入れ替えて得られる行列の行列式は－|A|である。つまり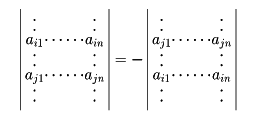

なお、列についても同様のことがいえる。この基本性質(4)から次のことがわかる。

(5)二つの行または列が等しい正方行列Aの行列式|A|は0である。

　また、(2)、(3)、(5)から
(6)正方行列Aの一つの行に他の行の定数倍を加えて得られる行列の行列式は|A|に等しい。つまり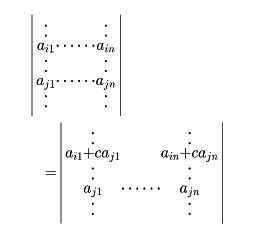

なお、列についても同様のことがいえる。与えられた行列式を計算するとき、この性質（6）を用いて、行列の成分に0を増やしたのち、計算公式や展開式を適用するとよい。

　行列の積と行列式の積については、
(7)二つの正方行列の積の行列式はそれぞれの行列の行列式の積に等しい。つまり
　　|A・B|＝|A|・|B|
［菅野恒雄］

行列式の展開公式

n次正方行列Aの第i行と第j列をAから取り去ってできる(n－1)次正方行列をA_ijとする。A_ijの行列式に(－1)^i+jを掛けたものã_ij＝(－1)^i+j|A_ij|を行列Aの(i, j)余因子という。基本性質を用いて次の展開定理が得られる。n次正方行列Aに対し
〔3〕|A|＝a_i1ã_i1＋a_i2ã_i2＋……＋a_inã_in
　　　(i＝1,……,n)
〔4〕|A|＝a_1jã_1j＋a_2jã_2j＋……＋a_njã_nj
　　　(j＝1,……,n)
　この式〔3〕〔4〕をそれぞれ、行列式|A|の第i行による展開公式、第j列による展開公式という。この公式により、n次の行列式の計算が(n－1)次の行列式の計算に帰着されることになる。基本性質(6)を用いて、一つの行なり列なりの成分に0を増やし、この展開公式を用いるとよい。

　さらに〔3〕はn²個のa_ijの恒等式とみなされ、ã_i1, ã_i2,……, ã_inはa_i1, a_i2,……, a_inを含まないから、(5)を用いると、次を得る。

〔5〕a_k1ã_i1＋a_k2ã_i2＋……＋a_knã_in＝0
　　　(k≠i)
同様にして〔4〕から次を得る。

〔6〕a_1kã_1j＋a_2kã_2j＋……＋a_nkã_nj＝0
　　　(k≠j)
いま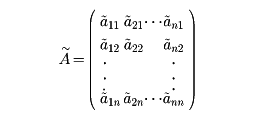

と置くと、〔3〕〔4〕〔5〕〔6〕からÃ・A＝A・Ã＝|A|・E_nが示される。ここで基本性質（7）と|En|＝1に注意すると、次のような行列式による正則行列の判定法と逆行列の計算方法を得る。つまり、正方行列Aが正則なるためには、その行列式|A|が0でないことが必要十分条件であり、このときAの逆行列A^-1は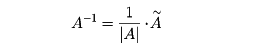

で求められる。

　なお、この式と〔5〕〔6〕から、連立一次方程式の解法の一般化であるクラメルの公式が出る。

［菅野恒雄］

小行列式

A＝(a_ij)を任意の(m, n)行列とする。mとnを超えない自然数pに対し、行列Aの任意のp個の行とp個の列をとり、その交点にあるp²個の成分からなるp次の正方行列を、たとえば次のようにつくる。

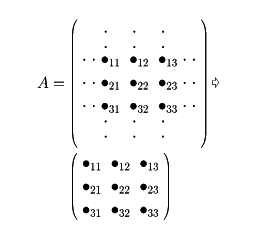
このようなp次の正方行列はmCp・nCp個あるが（mCpは異なるm個のもののなかからp個とる組合せを表す）、これらを行列Aのp次の小行列といい、その行列式をAのp次の小行列式という。上の展開式に現れたA_ijは（n－1）次の小行列であった。

　一般に（m, n）行列Aの0でない小行列式の最高次数は行列Aの階数（ランク）に等しい。この結果を用いて、行列Aの階数を小行列式の計算で得ることができる。

［菅野恒雄］

『斎藤正彦著『線型代数入門』（『基礎数学1』1966・東京大学出版会）』▽『佐武一郎著『行列と行列式』（1958・裳華房）』▽『寺田文行著『線形代数』（『サイエンスライブラリ　理工系の数学1』1974・サイエンス社）』

サラスの方法

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

行列式
ぎょうれつしき
determinant

n次の正方行列式 A＝（a_ij）に対して n次の行列式 detA（det(a_ij) あるいは｜A｜で表すこともあり，また detの代わりに D と書くこともある）を，
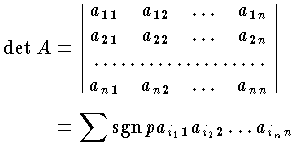と定義する。ただし，右辺のΣは次のような意味である。まず，A の主対角線上にある要素全部の積 a₁₁・a₂₂・…・a_nn をつくり，そこでこの各要素 a₁₁，a₂₂，…，a_nn の行を示す番号について，n!個の置換
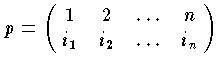を施す。この場合の i₁，i₂，…，i_n は 1，2，…，n を並べ替えて得られる順列である。もし p が偶置換ならばこのときの積の前に正符号＋を，奇置換ならば負符号－をつけることにする。ここで置換 p に対する符号を sgnp と書くことにすれば，行列式をつくる各項は，sgnpa_i11a_i22…a_innとなる。このようにして符号の定められた n!個の項全部の和が行列式 detA である。A が平面の線形変換を表すときは detA は面積比，3次元の線形変換のときは体積比を表し，一般に n次元の体積比を表す量と考えてよい。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

行列式【ぎょうれつしき】

n次の正方行列（行列）A＝（a(/i)(/j)）があるとき，各行からそれぞれ異なる列に属する要素を１個ずつとって掛け合わせた積の和をAの行列式といい，｜A｜，｜a(/i)(/j)｜，detA，det（a(/i)(/j)），または（式１）と書く。行列式の値は　a₁(/p)₁a₂(/p)₂…a(/n)(/p)(/n)符号（＋，−）をつけてすべてにわたって加えて求める。ここで（p₁，p₂，…，p(/n)）は（１，２，…，n）を入れ換えてできる順列（置換という）で，２個ずつの項の入れ換え（互換）を奇数回行ってできる順列（奇置換）ならば符号は−，偶数回でできる順列（偶置換）ならば＋とする。たとえば（式２）行列式のある一つの行（または列）の各要素をk倍すれば行列式はk倍になり，二つの行（または列）を入れ換えると符号が変わる。連立１次方程式の理論で重要。
→関連項目二次曲線｜ラプラス

出典　株式会社平凡社

世界大百科事典（旧版）内の行列式の言及

【生殖質】より

…1883年A.ワイスマンが提唱した生殖質説で想定した遺伝物質で，遺伝子に似た概念である。この説によれば生殖質は生物の遺伝と生殖に関与するデテルミナントdeterminant(決定要素)とよばれる単位から構成される。そして生殖細胞はその種に特有なあらゆるデテルミナントを含み，その構成を変化させることなく世代から世代へと伝達してゆく。…

【線形代数学】より

…一次独立と線形独立，一次写像と線形写像がそれぞれ同義であるのはその例である。線形代数学で扱う主対象は線形空間(ベクトル空間)，ベクトル，線形写像，アフィン空間，線形変換，行列，行列式，連立一次方程式などである。これらが主対象である理由は，これらの発生，発展が一次式に関連してなされてきたことにあるといえるが，その点をもう少し詳しく述べよう。…

※「行列式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」