世界大百科事典（旧版）内のgradientの言及
【こう配(勾配)】より
…微分可能な関数y＝f(x)で表される曲線が与えられたとき，その上の点(a,f(a))における曲線の接線はy－f(a)＝f’(a)(x－a)で表されるから，その接線のこう配はf’(a)である。
［ベクトル解析における関数のグラディエント］
二次元空間R2で定義された偏微分可能な関数f(x,y)に対して，(fx(x,y)，fy(x,y))なる成分をもつベクトル値関数(ベクトル場)をfのこう配，またはグラディエントgradientといい，gradfまたは∇fで表す。三次元空間R3で定義された関数f(x,y,z)に対しても，同様にベクトル値関数(fx,fy,fz)をgradfまたは∇fと書いて，fのグラディエントという。…
【ベクトル解析】より
…S上の点でのベクトル場Fのn成分をFnと書くことにし，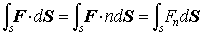
なる面積分を定義して，これをSを通過するベクトル流vector fluxという。
［勾配，発散，回転］
スカラー場φ(x,y,z)が与えられたとき，(∂φ/∂x，∂φ/∂y，∂φ/∂z)を成分とするベクトル場をφの勾配，あるいはグラディエントgradientと呼び，▽φ，またはgradφで表す。ベクトル場F＝(Fx,Fy,Fz)に対して，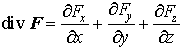
で定義されるスカラー場divFをFの発散といい，またx,y,z方向の単位ベクトルをそれぞれi，j，kとするとき，
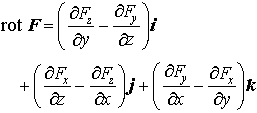で定義されるベクトル場rotF(curlFとも書く)をFの回転という。…
※「gradient」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」