一次独立（読み）いちじどくりつ

日本大百科全書(ニッポニカ)

一次独立
いちじどくりつ

いくつかのベクトルについて、それらの相互関係を述べるのに用いられる数学用語。一般にn個のベクトルa₁、a₂、……、a_nに対して
　　「l₁a₁＋l₂a₂＋……＋l_na_n＝0となるようなl₁、l₂、……、l_nはl₁＝l₂＝……＝l_n＝0しかない」
というとき、a₁、a₂、……、a_nは一次独立、あるいは線形独立であるという。たとえば、ベクトル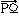と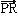は、3点P、Q、Rが同一直線上になければ一次独立である。また、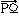、、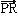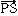は、4点P、Q、R、Sが同一平面上になければ一次独立である。a₁、a₂、……、a_nが一次独立であるということは、
　　「このなかのどの一つも、残りn－1個のベクトルを用いて、それらの“実数倍の和の形”に表されない」
ということと同義である。a₁、a₂、……、a_nが一次独立でないとき、a₁、a₂、……、a_nは一次従属あるいは線形従属であるといわれる。

［寺田文行］

[参照項目] | ベクトル

出典　小学館　日本大百科全書(ニッポニカ)