ポアソンのほうていしき
ポアソンの方程式
Poisson’s equation
Δφ=-4πρの形の2階偏微分方程式。ここでΔ=∂2/∂x2+∂2/∂y2+∂2/∂z2(ラプラシアン),ρは単位体積当りの湧き出しを表す関数である。いろいろな物理量に対して成り立つ。例えば,ρを密度とするとφは重力ポテンシャル,ρを電荷密度とするとφは静電ポテンシャルとなる。
執筆者:菊地 正幸
出典 平凡社「最新 地学事典」最新 地学事典について 情報
Sponserd by 
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
世界大百科事典(旧版)内のポアソンの方程式の言及
【楕円型方程式】より
…ここでuが未知関数,fは既知関数である。方程式(1)はポアソンの方程式とも呼ばれる。n次元空間Rnの中の2点x,yの距離をr(x,y)と書き,またRnの中の半径1の球面の表面積をωn(例えばω3=4π,ω4=4π2,ω5=4/3π2,……)と書くことにして,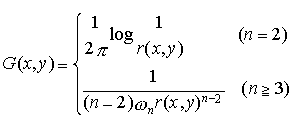 と定義する。…
と定義する。…
【偏微分方程式】より
… (4)においてfが変数tを含まない場合で,温度が平衡状態にあるとき,すなわちuが時間とともに変化しないときは,∂u/∂t=0であるから,(1/c)f(x)をあらためてf(x)と書けば,(4)は, Δu=-fとなる。この形の方程式を[楕円型方程式],またはポアソンの方程式という。とくにf≡0の場合の方程式Δu=0は,ラプラスの方程式と呼ばれる。…
【ポテンシャル】より
…微分することによって力が導かれるような場所の関数をポテンシャルと呼び,力学,電磁気学などの物理学において場を表すのに用いられる重要な概念である。ポテンシャルをU(x,y,z)とするとき,ベクトル解析の記号で力Fは, F=-∇U=-gradU ……(1) と表されるが,これはFのx,y,z方向の成分をFx,Fy,Fzとすると,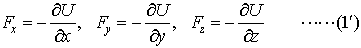 を意味している。このようにして与えられる力をとくに
を意味している。このようにして与えられる力をとくに[保存力]というが,それは,この力を受けて運動する質点の力学的エネルギー(運動エネルギーと位置エネルギーの和)が保存されるからである。…
【ポテンシャル論】より
… 例えば,三次元空間の,集合Eを占める物体Mがあり,点Q∈Eにおける密度がρ(Q)のとき,万有引力の定数をGとおけば,物体Mによる重力の場Fは,ポテンシャル,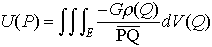 の-gradUに等しい。 P=P(x,y,z)とすると,この関数はポアソンの方程式,
の-gradUに等しい。 P=P(x,y,z)とすると,この関数はポアソンの方程式,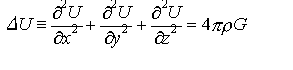 をみたす。したがって,とくに,Eの外点では⊿U=0をみたす。…
をみたす。したがって,とくに,Eの外点では⊿U=0をみたす。…
※「ポアソンの方程式」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 


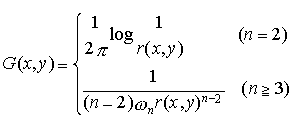 と定義する。…
と定義する。…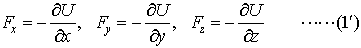 を意味している。このようにして与えられる力をとくに
を意味している。このようにして与えられる力をとくに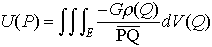 の-gradUに等しい。 P=P(x,y,z)とすると,この関数はポアソンの方程式,
の-gradUに等しい。 P=P(x,y,z)とすると,この関数はポアソンの方程式,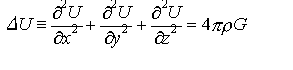 をみたす。したがって,とくに,Eの外点では⊿U=0をみたす。…
をみたす。したがって,とくに,Eの外点では⊿U=0をみたす。…