楕円型方程式（読み）だえんがたほうていしき（英語表記）elliptic equation

改訂新版　世界大百科事典

楕円型方程式 (だえんがたほうていしき)
elliptic equation

偏微分方程式の一つ。楕円型方程式の基本的な形は，

　Δu＝－f

　（Δ＝∂²/∂x₁²＋……＋∂²/∂x_n²）　……（1）　

と書かれる。ここでuが未知関数，fは既知関数である。方程式（1）はポアソンの方程式とも呼ばれる。n次元空間Rⁿの中の2点x，yの距離をr（x，y）と書き，またRⁿの中の半径1の球面の表面積をω_n（例えばω₃＝4π，ω₄＝4π²，ω₅＝4/3π²，……）と書くことにして，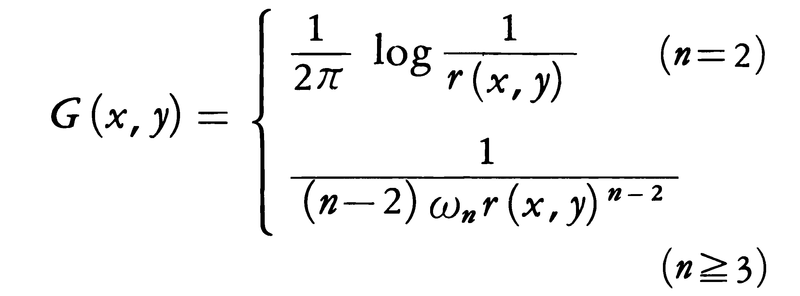

と定義する。（1）の右辺の関数f（x）が連続な1階偏導関数をもち，ある有界領域Dの外部では恒等的に0となるならば，関数，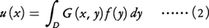

は（1）の解である。ここでdyはn次元の体積要素dy₁……dy_nを表す。（2）の関数uに，

　Δv＝0　……（3）　

を満たす関数vを加えたものも，やはり方程式（1）の解である。方程式（3）はラプラス方程式と呼ばれる。ふつうこのような問題は，与えられた領域Ωの内部で考察され，（3）の解はΩの境界上でのvの値（それを境界値という）を与えることによって定まる。例えばΩが平面上の単位円板の場合，その中の点を極座標（r，θ）で表し，Ωの境界（すなわち単位円周）上でのvの境界値v（1，φ）が与えられたとすると，（3）の解は，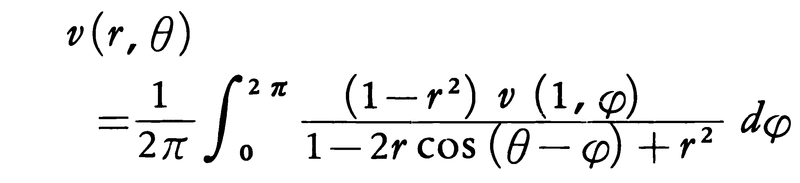

で与えられる。この右辺の積分をポアソン積分という。Ωが三次元空間の原点Oを中心とする単位球であるとき，Ωの内部の点xとΩの境界（すなわち単位球面）上の点yに対して，ベクトル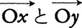とのなす角をγ_xyと書き，の長さをr_xと書くことにすると，球面上の境界値v（y）をとる（3）の解は，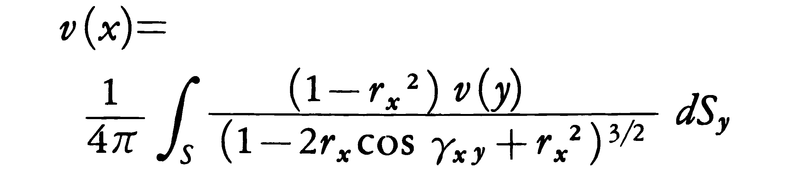

で与えられる。ここでSは単位球面，dS_yはその上での面積要素を表す。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内の楕円型方程式の言及

【偏微分方程式】より

…　(4)においてfが変数tを含まない場合で，温度が平衡状態にあるとき，すなわちuが時間とともに変化しないときは，∂u/∂t＝0であるから，(1/c)f(x)をあらためてf(x)と書けば，(4)は，　Δu＝－fとなる。この形の方程式を楕円型方程式，またはポアソンの方程式という。とくにf≡0の場合の方程式Δu＝0は，ラプラスの方程式と呼ばれる。…

※「楕円型方程式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」