ユニタリー行列（読み）ゆにたりーぎょうれつ（英語表記）unitary matrix

日本大百科全書(ニッポニカ)

ユニタリー行列
ゆにたりーぎょうれつ
unitary matrix

n次複素正方行列A=(a_ij)に対し、Ā=(ā_ij)の転置行列^tĀ=^t(ā_ij)を^*Aで表し、Aの随伴行列という。ここでā_ijは複素数a_ijの共役複素数である。とくにAが正則で、Aの逆行列A^-1が^*Aと等しいとき、つまり、
（1）A・^*A=^*A・A=E（Eはn次単位行列）
のとき、Aをユニタリー行列という。

　Aがユニタリー行列なら、次の（2）から（5）までが成り立つ。

（2）n次列ベクトル全体の線型空間Cⁿの線型変換T_A:Cⁿ∋x→Ax∈Cⁿは内積を不変にする。つまり、(Ax,Ay)=(x,y)　　(x,y∈Cⁿ)
（3）T_Aはベクトルの長さを不変にする。つまり
　　‖Ax‖=‖x‖　　(x∈Cⁿ)
（4）Aの列ベクトルは正規直交系である。つまり、A=(a₁,……,a_n)とすると、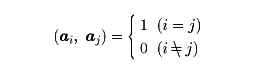

（5）^tAの列ベクトルは正規直交系である。

　逆に（2）から（5）のどれか一つが満たされればAはユニタリー行列である。また、実ユニタリー行列は、直交行列にほかならない。このように、ユニタリー行列、直交行列は、ともにベクトルの内積・長さと密接に関係するので、線型代数で非常に重要である。

［菅野恒雄］

出典　小学館　日本大百科全書(ニッポニカ)