直交行列（読み）ちょっこうぎょうれつ

日本大百科全書(ニッポニカ)

直交行列
ちょっこうぎょうれつ

Pをn次の正方行列で、成分は実数であるとする。Pの転置行列を^tPと書く。

　　^tPP=E　(Eはn次単位行列)
が成り立つとき、Pは（実）直交行列であるといわれる。二次の直交行列はすべて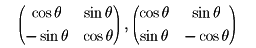

の形に表される。

　n項縦ベクトルの全体をRⁿと記す。Pがn次直交行列であるとき、任意のn項縦ベクトルxに対してPxを対応させる写像T_Pを（Pに対応する）Rⁿの直交変換という。

　　T_P(x)=Px　(x∈Rⁿ)
直交変換はRⁿの内積と距離を変えない。逆にRⁿの内積（したがって距離）を不変にするような線形変換は直交変換である。

　Aが実対称行列であるとする。すなわちAの(i,j)成分をa_ijとするとき、a_ijは実数で、
　　a_ji=a_ij　(i,j=1,2,……,n)
が成り立つものとする。このとき直交行列Pをうまくとれば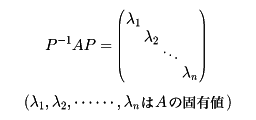

と表すことができる。右辺の行列の主対角線上の成分以外の成分はすべてゼロであるものとする。

［足立恒雄］

[参照項目] | 行列

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

直交行列
ちょっこうぎょうれつ
orthogonal matrix

正方行列 A の転置行列を ^tA とするとき，A^tA＝^tAA＝E ( E は単位行列) ならば，A を直交行列という。たとえば，単位行列は直交行列であり，また，
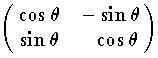も直交行列である。内積のあるベクトル空間の1次変換として考えれば，直交変換を表わす行列のことになる。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の直交行列の言及

【行列】より

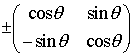…^tA＝Aとなるとき，Aは対称行列であるという。実行列で，^tA＝A^－1であるものを直交行列という。二次の直交行列は，であり，＋のほうは平面における原点のまわりの回転を表す。…

※「直交行列」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」