改訂新版 世界大百科事典 「エルミート形式」の意味・わかりやすい解説
エルミート形式 (エルミートけいしき)
Hermitian form
複素数αに対して,αの複素共役をᾱで表すことにする(α=a+biならばᾱ=a-bi)。āij=aji(1≦i,j≦n)をみたすn2個の数aijに対し,複素変数x1,x2,……,xnの式,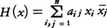 をエルミート形式という。H(x)は任意のx1,x2,……,xnに対し実数値をとる。aijを(i,j)成分とするn次正方行列とし,これをAと記す。n次正方行列Xに対して,Xの各成分の複素共役をとった行列の転置行列tをX*で表すものとすると,条件āji=ajiは,A=A*と表される。このような行列をエルミート行列Hermitian matrixという。行列Aの階数rをHの階数という。UU*=En(Enは単位行列)をみたすn次正方行列をユニタリ行列unitary matrixという。適当なユニタリ行列による線形変換(ユニタリ変換)
をエルミート形式という。H(x)は任意のx1,x2,……,xnに対し実数値をとる。aijを(i,j)成分とするn次正方行列とし,これをAと記す。n次正方行列Xに対して,Xの各成分の複素共役をとった行列の転置行列tをX*で表すものとすると,条件āji=ajiは,A=A*と表される。このような行列をエルミート行列Hermitian matrixという。行列Aの階数rをHの階数という。UU*=En(Enは単位行列)をみたすn次正方行列をユニタリ行列unitary matrixという。適当なユニタリ行列による線形変換(ユニタリ変換)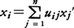 を行うと,正の実数αiが存在して,
を行うと,正の実数αiが存在して,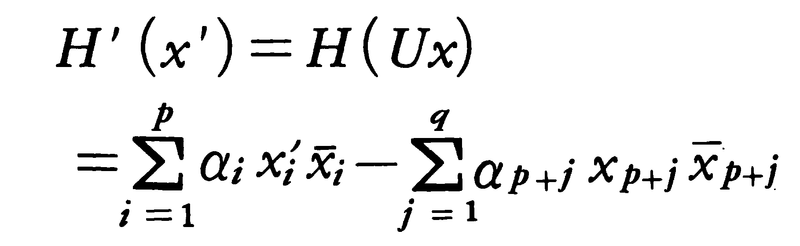
となる。このp,qはUの取り方にかかわらずに定まり,またp+q=rとなる。(p,q)をHの符号数という。(p,q)=(n,0)(または(0,n))のとき,正(または負)の定符号形式といい,それ以外のとき,不定符号形式という。
執筆者:斎藤 裕
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報

