ユニタリ変換（読み）ユニタリへんかん（英語表記）unitary transformation

改訂新版　世界大百科事典

ユニタリ変換 (ユニタリへんかん)
unitary transformation

n次元複素ベクトル空間Cⁿにおける一次変換は複素数を成分とするn次正方行列で表される。そのような行列A＝（a_ij）に対して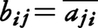，を成分とする行列（すなわちAの転置行列の複素共役）をAの随伴行列といい，A^＊で表す。U^＊U＝UU^＊＝1（単位行列）なる正方行列Uをユニタリ行列といい，ユニタリ行列で表されるCⁿの一次変換φをユニタリ変換という。Cⁿの二つのベクトル，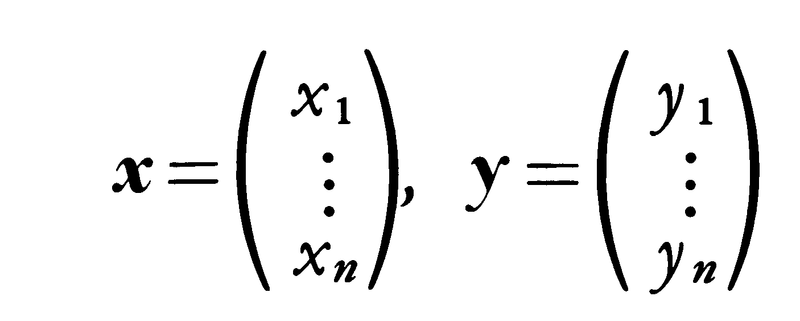

に対して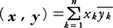，をxとyとの内積といい，また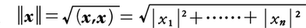，をxの長さという。ユニタリ変換φは内積および長さを不変にする。すなわち，（φ（x），φ（y））＝（x，y），／φ（x）／＝／x／。逆に，Cⁿにおける一次変換が内積を不変にすることと，長さを不変にすることとは同値であり，そのような一次変換はユニタリ変換である。ユニタリ変換はCⁿ全体を必ずCⁿ全体に写す。ユニタリ変換φを，対応するユニタリ行列の記号Uで表すこともある。例えば，上の〈長さを不変にすること〉を表す式を／Ux／＝／x／と書く。

　内積の定義された複素ベクトル空間の概念を無限次元に拡張したものがヒルベルト空間である。ヒルベルト空間Hにおける一次変換Uでベクトルの長さを不変にするものを等長変換というが，無限次元の場合は等長変換がHをH全体に写すとは限らない。ヒルベルト空間HをH全体に写す等長変換を，ユニタリ変換，またはユニタリ作用素という。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」