重心座標
じゅうしんざひょう
barycentric coordi-nate
n 次元ベクトル空間において,n+1 個の独立な点 A0,A1,…,An をとれば,この空間内の任意の点Xは,和が1である n+1 個の定数 λi により
X=λ0X0+λ1X1+…+λnXn
と表わすことができる。このとき数の組 (λ0,λ1,…,λn) を点Xの重心座標という。それは,この n+1 個の点 Ai に λi の重みを与えたときの重心がXになるからである。特に λi がすべて正または0であるときに限定して使うこともある。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
世界大百科事典(旧版)内の重心座標の言及
【座標】より
…これを円柱座標cylindrical coordinatesという(図9)。
[重心座標barycentric coordinates]
空間内に同一平面上にない4点A0,A1,A2,A3が与えられたとき,空間内に1点Oをとり,ベクトル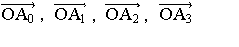 を考えれば,空間内に点Pがあるとき,
を考えれば,空間内に点Pがあるとき,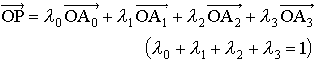 となる実数の組(λ0,λ1,λ2,λ3)が定まり,これはOのとり方によらない。(λ0,λ1,λ2,λ3)を点Pの重心座標という。…
となる実数の組(λ0,λ1,λ2,λ3)が定まり,これはOのとり方によらない。(λ0,λ1,λ2,λ3)を点Pの重心座標という。…
※「重心座標」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 


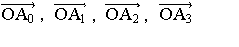 を考えれば,空間内に点Pがあるとき,
を考えれば,空間内に点Pがあるとき,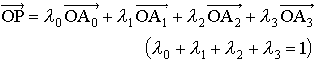 となる実数の組(λ0,λ1,λ2,λ3)が定まり,これはOのとり方によらない。(λ0,λ1,λ2,λ3)を点Pの重心座標という。…
となる実数の組(λ0,λ1,λ2,λ3)が定まり,これはOのとり方によらない。(λ0,λ1,λ2,λ3)を点Pの重心座標という。…