精選版 日本国語大辞典 「重心」の意味・読み・例文・類語
じゅう‐しんヂュウ‥【重心】
- 〘 名詞 〙
- ① 物体の各部分に働く重力の合力が作用するとみなされる点。質量中心と一致する。重力中心。
- [初出の実例]「体各有レ重、重各有二中心一」(出典:気海観瀾(1827))
- 「働の一方に重心を偏し、無理によく之を名状すれば」(出典:文明論之概略(1875)〈福沢諭吉〉六)
- ② 数学で、図形F上に一様に質量を分布させたときの質量中心のFに対する称。三角形のそれをさすことが多い。後者は、三つの中線の交点と一致する。〔数学ニ用ヰル辞ノ英和対訳字書(1889)〕
- ③ ものごとの中心となる点。また、重点。
- [初出の実例]「クラを重心にして一家は運営できないし」(出典:欅の芽立(1936)〈橋本英吉〉一)
重心の語誌
この語は明末に中国に渡ったイエズス会士らによる「遠西奇器図説」に見られる。この洋学書は、江戸期に日本に伝わり、広く蘭学者たちに読まれた。「重心」はこの時期に日本に伝来した新語。
改訂新版 世界大百科事典 「重心」の意味・わかりやすい解説
重心 (じゅうしん)
(1)数学の重心barycenter 空間にn個の点A1,A2,……,Anがあるとき,1点Oをとってベクトル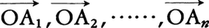 を考え,w1≧0,w2≧0,……,wn≧0,w1+w2+……+wn=1を満たす実数w1,w2,……,wnに対して,
を考え,w1≧0,w2≧0,……,wn≧0,w1+w2+……+wn=1を満たす実数w1,w2,……,wnに対して,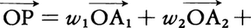
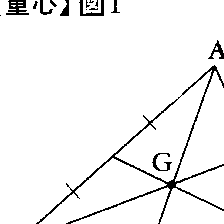
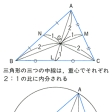
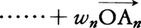 を満たす点Pをつくれば,PはOのとり方によらない。この点PをA1,A2,……,Anに重みw1,w2,……,wnをつけたときの重心といい,とくにw1=w2=……=wn=1/nのときのPを単にA1,A2,……,Anの重心という。異なる2点A,Bの重心は線分の中点,すなわち線分ABを2等分する点である。1直線上にない3点A,B,Cの重心Gを三角形ABCの重心(図1),1平面上にない4点A,B,C,Dの重心Gを四面体ABCDの重心(図2)と呼ぶ。三角形の各頂点を対辺の中点に結ぶ線分は三角形の重心を通り,この点で2:1の比に内分される。四面体の各頂点を対面の重心に結ぶ線分は四面体の重心を通り,この点で3:1の比に内分される。
を満たす点Pをつくれば,PはOのとり方によらない。この点PをA1,A2,……,Anに重みw1,w2,……,wnをつけたときの重心といい,とくにw1=w2=……=wn=1/nのときのPを単にA1,A2,……,Anの重心という。異なる2点A,Bの重心は線分の中点,すなわち線分ABを2等分する点である。1直線上にない3点A,B,Cの重心Gを三角形ABCの重心(図1),1平面上にない4点A,B,C,Dの重心Gを四面体ABCDの重心(図2)と呼ぶ。三角形の各頂点を対辺の中点に結ぶ線分は三角形の重心を通り,この点で2:1の比に内分される。四面体の各頂点を対面の重心に結ぶ線分は四面体の重心を通り,この点で3:1の比に内分される。
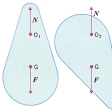
執筆者:中岡 稔(2)力学の重心center of gravity 物体の各部分に作用する重力の合力の作用点。質量中心center of massともいう。物体の全質量をM,重力の加速度をg,重心をGとすると,重力の合力はGに働く大きさMgの力になるから,G点の真上を上向きにMgの力で支えれば物体はつり合う。物体を糸でつるしたとき,重心は糸の延長線にくるはずだから,2ヵ所以上を選んでそれぞれのところでつるせば,糸の延長線の交点から重心を求めることができる(図3)。図4のように質量を無視できる軽い棒の両端に質量m1,m2のおもりをつけたものを支えるには,m1が棒を右に回そうとするモーメントm1gl1とm2が棒を左に回そうとするモーメントm2gl2のつり合うG点(m1l1=m2l2の点)をつるせばよい。もっとたくさんのおもりをつないだ図5の場合には,モーメントのつり合いは,m1(x1-X)+m2(x2-X)+m3(x3-X)=m4(X-x4)+m5(X-x5)と表されるから,重心のx座標Xは,m1x1+m2x2+……+m5x5=(m1+m2+……+m5)Xを満たすことがわかる。つまりXは,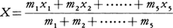 で与えられる。おもりの数はもっと多くても同じであるし,糸を90度回しても同じGでつり合うから,重心の位置(X,Y,Z)を求める一般式として,
で与えられる。おもりの数はもっと多くても同じであるし,糸を90度回しても同じGでつり合うから,重心の位置(X,Y,Z)を求める一般式として,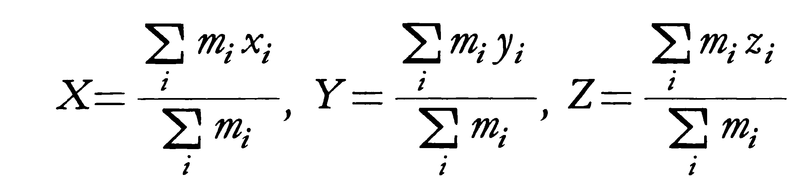
が得られる。連続的な物体も,細分して多数の小片からできていると考えれば,同じやり方で重心が求められる。計算には積分が使われる。
大きさのある物体が外力によって運動するときに重心の行う運動は,物体の全質量と同じ質量をもつ質点に外力の合力が加えられたと仮定した場合に,その質点が行う運動に等しい。したがって,物体を質点とみなすのは,重心運動だけに着目するということにほかならない。
執筆者:小出 昭一郎
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「重心」の意味・わかりやすい解説
重心
じゅうしん
数学用語
三角形の重心
三角形の三つの中線は1点で交わる。その点を三角形の重心という。三つの中線は重心でそれぞれ2対1の比に内分される。三角形の重心、垂心、外心は1直線上にある。三角形の重心は三つの頂点を等質量の質点と考えた場合の力学的な意味での重心でもある。また、三角形の重心は、三角形を密度が均一な板と考えたときの力学的重心でもある。しかし、三角形の重心は、三角形の周を等質量の質点の集まりと考えたときの物理的な意味での重心とは一般には一致しない。
四面体の重心
四面体の各頂点と相対する面である三角形の重心とを結ぶ四つの直線は1点に交わる。この点を四面体の重心という。この点で頂点と対面の重心とを結ぶ線分は3対1の比に内分される。四面体の重心は四つの頂点を等質量の質点と考えたときの力学的重心であり、また、四面体を密度が均一の剛体と考えたときの力学的重心でもある。
n個の点の重心
平面上あるいは空間にあるn個の点の重心とは次のように帰納的に定められる。k個の点の重心が定まったとき、k+1番目の点とk個の点の重心とを結ぶ線分をk対1に内分する点がk+1個の点の重心である。2点の重心はその中点であることから始めて逐次3点、4点、……の重心が定められる。これはn個の点を等質量の質点と考えたときの力学的重心でもある。
[柴田敏男]
物理学用語
物体を構成する質点の、以下に述べるような意味での平均的な位置が重心の位置を与える。この平均としては、各質点の質量を重荷とする重荷平均をとる。物体の各質点に働く重力の重心の周りのモーメントの和はゼロである。したがって、各質点に働く重力が重心に集まって働いていると考えてもよい。重心とよぶのは、この性質のためである。物体が運動するとき、物体の全質量と重心の加速度との積は、外力の合力に等しい。一般に物体の運動は、重心の運動と、物体の各質点が重心に対して行う相対運動とからなる、とみなすことができる。
2個の粒子の衝突を論ずるにあたって、実験室に固定した座標系(実験室系)を用いることもあるが、二つの粒子の重心を座標原点とするような座標系(重心系)を用いることもある。重心系を用いると、二つの粒子の運動量(質量と速度の積)はつねにその大きさと方向が等しく、向きが逆向きになる。
[飼沼芳郎]
ブリタニカ国際大百科事典 小項目事典 「重心」の意味・わかりやすい解説
重心
じゅうしん
center of gravity
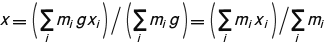 を x 座標とする点を通る。 y ,z 座標についても同様であるから,重力の合力は次の座標をもつ点を通る。
を x 座標とする点を通る。 y ,z 座標についても同様であるから,重力の合力は次の座標をもつ点を通る。 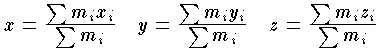 この点が重心である。前式は質量 mi を統計的重率とした座標 xi ,yi ,zi の平均位置を表わすので質量中心とも呼ばれる。密度が一様で対称な物体の重心は,その対称軸または対称面の上にある。
この点が重心である。前式は質量 mi を統計的重率とした座標 xi ,yi ,zi の平均位置を表わすので質量中心とも呼ばれる。密度が一様で対称な物体の重心は,その対称軸または対称面の上にある。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「重心」の意味・わかりやすい解説
重心(物理)【じゅうしん】
→関連項目重心(数学)
出典 株式会社平凡社百科事典マイペディアについて 情報
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...