全射（読み）ゼンシャ（英語表記）surjection

デジタル大辞泉

ぜん‐しゃ【全射】

数学で、集合A・Bにおいて、Bのどの要素に対してもAの要素が対応する写像。

出典　小学館

精選版 日本国語大辞典

ぜん‐しゃ【全射】

1. 〘 名詞 〙 数学で、全体へ写す写像。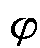が集合Ａから集合Ｂへの写像で、Ｂのいかなる元ｂに対しても、Ａの適当な元ａをとれば 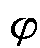(a)=b となるとき、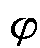をＡからＢへの全射という。

出典　精選版 日本国語大辞典

ブリタニカ国際大百科事典 小項目事典

全射
ぜんしゃ
surjection

集合 S₁ から S₂ への写像を f：S₁→S₂ とするとき，f によって写された S₁ の像が S₂ 全体であるとき，すなわち S₂ の任意の元 y に対して f(x)＝y であるような S₁ の元 x が少くとも1つ存在するとき，写像 f は全射あるいは S₁ から S₂ の上への写像 onto-mappingであるという。

出典　ブリタニカ国際大百科事典 小項目事典

改訂新版　世界大百科事典

全射 (ぜんしゃ)

→写像

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内の全射の言及

【写像】より

…また，Bの部分集合B′に対し，Aの元でfによる像がB′の中に入るもの全体｛a∈A｜f(a)∈B′｝を，fによるB′の原像，あるいは逆像といい，f^－1(B′)で表す。
［全射，単射，全単射］
　写像f：A→Bにおいて，fの像f(A)がBと一致するとは限らない。そこで，f(A)＝Bが成り立つとき，すなわち，Bのどの元bについても，bをfの値とするAの元aが，少なくとも一つ存在するとき，fはAからBへの全射，あるいはAからBの上への写像であるという。…

※「全射」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」