放物型方程式（読み）ほうぶつがたほうていしき（英語表記）parabolic equation

改訂新版　世界大百科事典

放物型方程式 (ほうぶつがたほうていしき)
parabolic equation

偏微分方程式の一つである放物型方程式の基本的な形は，

　∂u/∂t＝c⊿u＋f（t，x）　……（1）　

　　（t＞0，⊿＝∂²/∂x₁²＋……＋∂²/∂x_n²）

と書かれる。ここでcは正の定数，fは既知関数である。物理的には熱伝導，または物質の拡散現象を記述する方程式で，未知関数u＝u（t，x）は時刻t，空間の点x＝（x₁，……，x_n）における温度，または拡散物質の濃度を表す。通常，方程式（1）の解で初期条件，

　u（0，x）＝u₀（x）　　　……（2）　

を満たすものを求めることが問題になる。ここでu₀（x）は有界連続な関数で，初めの温度分布，または濃度分布を表す。この問題を放物型偏微分方程式の初期値問題という。この初期値問題の解u（t，x）は，基本解と呼ばれる関数，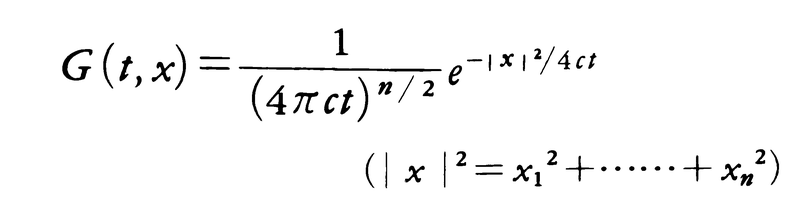

を用いて，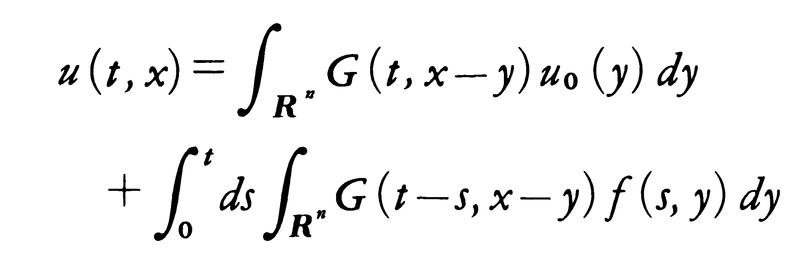

により与えられる。ここでdyはn次元空間Rⁿにおける体積要素dy₁……dy_nを表し，Rⁿの点x＝（x₁，……，x_n），y＝（y₁，……，y_n）に対して，x－yは点（x₁－y₁，……，x_n－y_n）を表す。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内の放物型方程式の言及

【偏微分方程式】より

…ここでcは熱伝導率などによって定まる正の定数であり，fは外部から熱が供給される状態を表す既知関数である。(4)の形の方程式は放物型方程式，または熱伝導方程式と呼ばれる。また物質の拡散現象においても，その物質の濃度uの変化は(4)の形の方程式で記述されるので，この方程式を拡散方程式とも呼ぶ。…

※「放物型方程式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」