関数（読み）カンスウ

デジタル大辞泉

かん‐すう〔クワン‐｜カン‐〕【関数／^×函数】

１ 《function》二つの変数x、yがあって、xの値が決まると、それに対応してyの値が一つ決まるとき、yはxの関数であるという。記号y＝f（x）で表す。xを独立変数といい、二つ以上のこともある。また、この概念を拡張して、ある集合の各要素に他の集合の各要素を一対一で対応させる規則である写像をさすこともある。
２ コンピューターのプログラミング言語やアプリケーションソフトにおいて、ある数や文字列が入力された時、決められた処理を行い、その結果を出力する命令群のこと。

出典　小学館

精選版 日本国語大辞典

かん‐すうクヮン‥【関数・函カン数】

1. 〘 名詞 〙 ( [英語] function の訳語 )
2. ① 変数ｙが変数ｘの変化に関連して、従属的に変化する時の、ｙのｘに対する称。ｘを独立変数といい、二つ以上のこともある。また、比喩的に、ある物の変化に伴って、他の物も変化するような場合、後者を前者に対していう。〔哲学字彙（1881）〕
3. ② 一つの集合の各要素に、他の集合の要素を一つずつ対応させる規則の称。写像。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

関数 (かんすう)

この言葉はかつては〈函数〉と書かれたが，これは英語functionの中国語における音訳で，現在は〈関数〉と書かれることが多い。

　例えば，半径rの円の面積をSとすると，S＝πr²という関係があり，rの値を定めると，それに対応してSの値が定まる。このように，ある範囲にわたって変化する量xのおのおのの値に対して，別のある量yの値を対応させる規則が定められているとき，yはxの関数であるという。またその対応規則のことを関数と呼び，f，g，φなどの記号を用いてy＝f（x）のように表す。具体的な書き方としては，例えばxにy＝2x²＋3を対応させる関数をf（x）＝2x²＋3と書く。

　g（x）＝sinx，h（x）＝logx

なども関数の例であるが，関数は必ずしもこのような式で表される必要はなく，

　φ（x）＝xグラムの定形外封書の郵便料金（単位は円）

も関数である。

関数の一般的定義

前述の関数の概念を一般化して，関数を次のように定義する。

　二つの集合X，Yがあって，Xのどの要素xにも，Yの要素yがちょうど一つ対応しているとき，この対応をXからYへの関数，または写像といい，記号fなどを用いて，f：X→Yと書いたり，y＝f（x）と書いたりする。前に述べたいくつかの例は，いずれもX，Yが実数の集合の場合であるが，x，yが必ずしも数ではなくても，xを変数と呼び，yはxの関数であるということが多い。

　関数f：X→Yにおいて，集合Xを関数fの定義域といい，Xの各要素に対応するYの要素全体が作る集合を，関数fの値域という。前に述べた例では，関数f，gの定義域は実数全体であるが，hの定義域は正の数全体である。また，hの値域は実数全体であるが，f，gの値域はそれぞれx≧3なる実数xの全体，｜x｜≦1なる実数xの全体である。前例の関数φについては，定義域は0≦x≦1350なる実数xの全体であり，値域は有限集合，

　｛120，140，160，200，240，270，　　390，580，700｝

である（ただし，1997年3月現在）。なお，関数が数式で表されている場合，定義域は必ずしもその数式が意味をもつ変数の値の全体と考えなくてもよい。例えば，最初にあげた円の半径にその面積を対応させる関数S＝πr²は，数式としてはすべての実数rに対して意味があるが，この関数の定義域は正の数rの全体と考える。

関数概念の歴史

関数という語を初めて用いたのはG.ライプニッツで17世紀末であった。彼は明確には定義しなかったが，変数とともに変動する量を考えて関数と呼んだ。その後ヨハン・ベルヌーイが，変数と定数とからなる算式のことを関数といった。次いで1748年オイラーが，変数と定数とからなる解析的な式として関数を定義し，xの関数を表す記号f（x）を導入した。1823年A.コーシーは，式で表されるかどうかに関せず，上記の対応という概念のもとに，形式上は一般的な関数の定義に到達したが，彼自身はまだ対応の関係としては，それがいくつかの解析的な式で表されることを暗に仮定していたようである。P.ディリクレ，G.リーマンに至って，初めて現在行われている上記の一般的定義に達したといえる。ただし，上記のように集合と言葉を用いて表されたのは，集合論ができた19世紀末以後のことである。

1変数の関数，多変数の関数

関数fの定義域，値域が実数の集合である場合は，定義域の中の一つの実数xを与えると関数の値y＝f（x）が定まるから，このような関数を1変数の関数という。これに対して，定義域がn次元空間の点の集合である場合は，そのような点はn個の実数（x₁，……，x_n）によって表されるから，その点の関数はy＝f（x₁，……，x_n）の形に表される。このような関数をn変数の関数という。n＝1ならば前に述べた1変数の関数であるが，n≧2の場合を多変数の関数という。とくにn＝2，3の場合にはz＝f（x，y），w＝f（x，y，z）などの表し方をする。例えばz＝x²＋y²は2変数の関数である。

　さらに，関数fの値域がm次空間の中の集合である場合は，その値yはm個の実数（y₁，……，y_m）で表されるから，関数fはm個の実数値関数の組，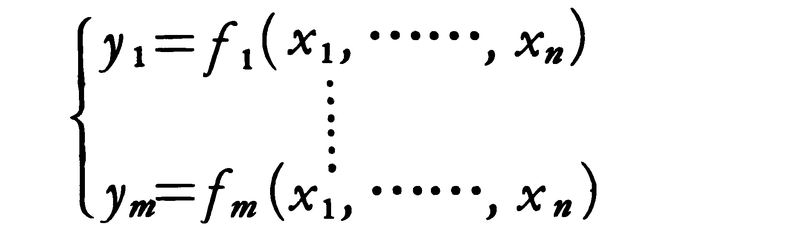

で表される。これに対し，定義域が実数の集合で値域がm次元空間（m≧2）の中の集合である場合も考えられる。例えばm＝2のとき，実数tの関数の組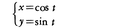，は，定義域が実数の全体，値域が二次元空間，すなわち平面の中の集合（この場合は単位円周：x²＋y²＝1）である関数を与える。

陰関数，陽関数

2変数の関数F（x，y）が与えられていて，F（x，y）＝0という関係によってyがxの関数として定まるとき，それを陰関数という。これに対し，上記のようにy＝f（x）の形に表される関数を陽関数という。F（x，y）＝0なる関係式から，yについて解くことによりy＝f（x）の形の表現が得られれば，これは陽関数として表されたわけで，陰関数と陽関数とは表現上の相違に過ぎない。これらの名称は関数を解析的な式で表されるものと考えた時代に生じたものであるが，陰関数という言葉は記述の便宜上現在でも使われている。

多価関数

例えばx²＋y²＝1なる関係式があるとき，｜x｜＜1なるxに対しては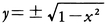，なる二つのyの値が定まる。このyをxの関数として取り扱うとき多価関数というが，これは（本来の意味の）関数としては｜x｜≦1を定義域とする二つの関数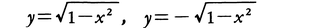，と考えればよい。なお，解析関数の多価性については〈リーマン面〉の項目を参照。

関数と写像

現代数学における用語としては，関数と写像とはまったく同義語であるが，歴史的習慣により，値域が実数または複素数の集合である場合には関数と呼ぶことが多い。定義域が関数の集合であって，値域が実数または複素数の集合である場合には，汎（はん）関数と呼ぶことがあるが，これも歴史的理由による。これらの名称は，その内容を直観的にわかりやすくしていて便利なので，現代でもふつうに使われている。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

関数
かんすう
function

昔は「函数」と書いた。二つの変数x、yがあって、xの値が決まれば、それに伴ってyの値がただ一つ決まるとき、yはxの関数であるという。

　たとえば、1個a円のりんごx個の値段をy円とすれば、y＝axであり、この式によってyはxの関数として定められる。また郵便料金の場合、xグラムの書状の料金をy円とすれば、yをxについての一つの式だけで表すことはできない。しかし各xに対してyの値はただ一つ決まるからyはxの関数である。この二つの例をみると、第一の例では、変数xは1個、2個、3個……というように整数値、つまり、ばらばらな値（離散的という）しかとらない。第二の例では、xの値は整数値とは限らない（つまり、連続的な値をとる）。また、どちらの例でもxの値についてはその大きさについて常識的な限度を設けて考えるのが普通である。このように、日常の事例に関連する数理としては、変数xのとりうる値の範囲については漠然とした約束があるが、それだけでは数学の対象とはなりえないので、変数xがとることのできる値の範囲を決める。これを関数の定義域といい、関数のとる値全体の集合を値域という。

　関数の定義域としては、0≦x≦1であるような実数全体の集合、1≦x≦100であるような整数全体の集合などという与え方もあるが、関数が式で示されたとき、その関数がとりうる最大の範囲をその関数の定義域と考えることも多い。たとえば、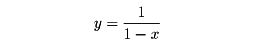

では、定義域はx≠1であるような実数全体、

では、定義域はx≦1であるような実数全体を考える。yがxの関数であることを一般的に表す方法として、y＝f(x)あるいはg(x), F(x)などが用いられる。

［竹之内脩］

合成関数

関数は単独でも用いられるが、いくつかの関数を組み合わせて考えることも多い。関数f(x), g(x)の和、差、積、商などを考えるだけでなく、二つの関数を合成するという操作もよく用いられる。すなわち、g(f(x))というものが定義できれば、これで新たな関数ができあがる。たとえば、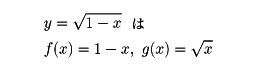

の合成関数として得られた関数である。また、yがxの関数であるとき、逆に、xをyの関数と考えることのできる例も多い。これが逆関数であり、この考察は実用上重要である。

［竹之内脩］

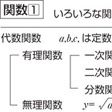
いろいろな関数

f(－x)＝f(x)を満たす関数を偶関数、f(－x)＝－f(x)を満たす関数を奇関数という。関数y＝f(x)において、xの値が増加すれば対応するyの値も増加するとき増加関数、xの値が増加すればyの値が減少するとき減少関数という。関数は、その特徴を表すために、いろいろな名前をつけてよばれることが多い。xの多項式によって表される関数を有理整関数、xの分数式で表される関数を分数関数、あるいは有理関数といい、根号の加わった関数を無理関数という。なお、微分積分学で基本的であると考えられる関数を初等関数というが、これには、三角関数、指数関数、対数関数などがある。

　いままでは1変数xの関数を考えてきたが、いくつかの変数（多変数）x₁, x₂,……, x_nに対し、これらの値を決めれば、それに伴ってyの値がただ一つ定まるとき、yはx₁, x₂,……, x_nの関数であるという。物理学で空間（三次元）の現象を問題にするときは、3変数x, y, zの関数が考察される。また経済学では、数多くの変数（需要量、供給量、生産量、雇用量、貯蓄性向、消費性向など）を考えることが多い。

［竹之内脩］

関数概念の発達

古くから考えられた関数は平方根で、4000年ぐらい昔にさかのぼることができよう。ついで三角関数が2000年ぐらい昔に考えられている。17世紀になってネーピアが対数を考えた。このようにみていくと、関数の概念は、ものの数量的把握の方法として、きわめて自然に発生し、形成されてきたといえよう。関数ということばをつくったのは17世紀末のライプニッツで、原語の意味は働き、機能ということである。xの値にyの値を一つずつ対応させる働きという認識だったのだろうが、まだ、そのように明確な形では表現されてはいない。オイラーなどは、関数すなわち式と考えて、関数を式の形で分類している。18世紀から19世紀にかけて関数概念がさらに明確化され、整理されていくなかで、この項の初めに述べたような形の定義が登場する。これはディリクレに負うものであって、1837年のことであった。今日ではさらに広く考えて、一つの集合から他の集合への写像のことも関数とよぶ風潮がある。しかし、関数本来の考え方からいえば、変数xの値が動いていく、それに伴ってyの値も動いていく、というところに関数概念の中心があるといえる。

［竹之内脩］

[参照項目] | 逆関数 | 三角関数 | 指数関数 | 初等関数 | 対数関数

いろいろな関数

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

関数
かんすう
function

17世紀に近代数学が成立して以来，変化の法則性をとらえることが課題になり，それにはある領域 Aを動く xを変数として，xに対応する別の領域 Bの変数 y＝f(x)を考えるようになった。この場合 xに yが対応しているという関係は，グラフ {(x，y)|y＝f(x)} でとらえられるが，最初の変数（独立変数）xに応じてあとの変数（従属変数）yが定まっているという点に，xと yとの関係（関数関係）の特別の場合として以上の強調がある。G.W.ライプニッツが最初に関数の概念を使った頃は，functio（ラテン語）は変化する諸量を意味し，これらは混同されていたが，y＝2x＋3のような式で関数を表すことと，一般のグラフで関数を表すこととの混乱を整理するため，19世紀中頃，特に ピーター・G.L.ディリクレ以降は，対応そのものの fを問題にするようになり，さらにそれ自体を元として関数空間を考えたりするようになってきた。xや yは数だけでなく，ベクトルや一般の空間の点などを表すときにも使う。そのとき，xのほうが実（または複素）n次元空間の点のとき実（または複素）n変数関数と呼び，yが実数，複素数，ベクトルのときには実数値，複素数値，ベクトル値関数のようにいう。現代数学では，関数を表示するときは f:A→Bのように書くのが普通で，Aを域 domainまたは始集合 initial set，Bを余域 codomainまたは終集合 final setという。また，伝統的には，Aを定義域 domain，Bではなくて像 f(A) を値域 rangeということもある。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

関数【かんすう】

二つの変数x，yにおいてxの値が定まればyの値が定まるとき，yをxの関数といい，y＝f（x）と書く。xを独立変数，yを従属変数という。また一般にx₁，……，x(/n)の値が定まればyの値が定まるときyをx₁，……，x(/n)の（n変数の）関数といい，y＝f（x₁，……，x(/n)）と書く。関数y＝f（x）が定義されるx（またはx₁，……，x(/n)）の値の範囲をf（x）の定義域，yのとる値の範囲をf（x）の値域という。xの一つの値に対しyの値がただ一つ定まるときはこの関数を１価関数といい，二つ以上定まるときは多価関数という。→関数論／陽関数／陰関数／奇関数／写像
→関連項目逆関数｜逆三角関数｜グラフ｜変数｜森毅

出典　株式会社平凡社

知恵蔵

関数

数学では、データを入力するとブラックボックスを通って結果が出力される、という状況にしばしば出会う。このブラックボックスを関数という。17世紀後半、ライプニッツ(G.W.F.Leibniz)が英語のfunctionのもとになるイタリア語のfunctioを使ったのが始めとされる。本来は函数という漢字が用いられていたが、これは中国語の発音でfunctionの音訳であるとされている。三角関数、指数関数、対数関数など。また、写像という用語は、関数とほとんど同義に用いられる。

(桂利行 東京大学大学院教授 ／ 2007年)

出典　(株)朝日新聞出版発行「知恵蔵」

パソコンで困ったときに開く本

関数

数学の「関数」と同じ意味です。表計算ソフトなどでは、あらかじめ計算式やデータ処理に名前が設定されていて、セル内でその名前を呼び出すと計算やデータ処理を行い、結果をそのセルに表示します。
⇨表計算ソフト

出典　(株)朝日新聞出版発行「パソコンで困ったときに開く本」

世界大百科事典（旧版）内の関数の言及

【関数解析学】より

…19世紀の終りごろまでは，関数はおもにその各点における値に着目して研究されてきたが，20世紀に入って集合論の発祥とともに，ある条件を満たす関数全体の集り(集合)を考え，個々の関数をその集合の要素として扱う考え方が行われるようになった。そうして，ふつうのユークリッド空間でベクトルの加法や定数倍の算法を考えたり，点列がある1点に近づくという〈収束〉の概念を用いたりするのと同様に，関数の集合の中でベクトルの算法や収束を考える。…

※「関数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」