偏微分方程式（読み）ヘンビブンホウテイシキ（英語表記）partial differential equation

デジタル大辞泉

へんびぶん‐ほうていしき〔‐ハウテイシキ〕【偏微分方程式】

偏導関数を含む微分方程式。これに対し、導関数だけを含むものを常微分方程式という。

出典　小学館

精選版 日本国語大辞典

へんびぶん‐ほうていしき‥ハウテイシキ【偏微分方程式】

1. 〘 名詞 〙 微分方程式の一つ。未知関数が多変数の関数で、未知関数の偏導関数を含むものをいう。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

偏微分方程式 (へんびぶんほうていしき)
partial differential equation

三次元空間の各点P（x，y，z）においてベクトルa（P）が与えられていて，その成分が，

　a（x，y，z），b（x，y，z），

　c（x，y，z）

であるとする。この空間内の曲面，

　z＝u（x，y）　……（1）　

で，その上の各点P（x，y，z）において与えられたベクトルa（P）が，その曲面に接するようなものを求めるという問題を考える。曲面（1）の上の点P（x，y，u（x，y））におけるその曲面の法線ベクトルは（u_x，u_y，－1）と表され，a（P）が曲線（1）に接するということは，この法線ベクトルがa（P）に垂直なことであるから，その条件は方程式，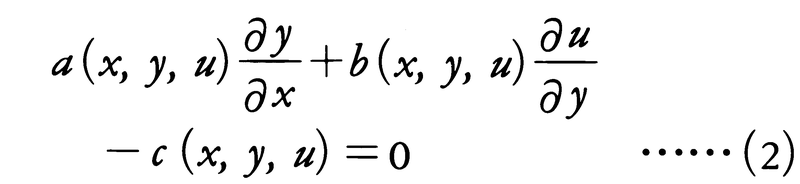

で与えられ，これを満たす関数u（x，y）を求めれば，初めの問題が解けたことになる。このように未知関数の偏導関数を含む方程式を偏微分方程式という。

　方程式（2）は次のようにして解ける。連立常微分方程式，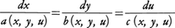

の解は一般に二つのパラメーターα，βを含む，

　x＝f（u;α，β），y＝g（u;α，β）　……（3）　

の形に書ける。（3）はxyu空間の一つの曲線を表すので，これを（2）の特性曲線という。（3）をα，βについて解いたものをα＝φ（x，y，u），β＝ψ（x，y，u）とすると，これを任意関数β＝F（α）に代入して得られる関係式が（2）の一般解である。任意関数Fは初期条件によって定められる。例えば，

の解で初期条件y＝0のときu＝\(\frac{x}{a}\)を満たすものを求めてみよう。特性曲線は，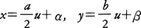

となるから，一般解は，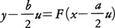

これに初期条件を代入して，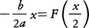

したがって，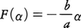

となるから，求める解は，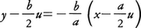

すなわち，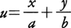

　一般に方程式の中に現れる未知関数の偏導関数の中で，偏微分の階数の最高がnならば，n階偏微分方程式という。例えば（2）は1階偏微分方程式である。2階偏微分方程式は次のような数理物理学の問題に現れる。

　空間の点x＝（x₁，x₂，……，x_n）の関数u（x）に対して，ラプラシアンLaplacianと呼ばれる偏微分演算子Δを，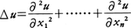

によって定義する。nはその空間の次元である。

熱伝導の問題

時刻t，空間の点xにおける温度u（t，x）が熱伝導によって時間とともに変化していくとき，その変化は方程式，

によって記述される。ここでcは熱伝導率などによって定まる正の定数であり，fは外部から熱が供給される状態を表す既知関数である。（4）の形の方程式は放物型方程式，または熱伝導方程式と呼ばれる。また物質の拡散現象においても，その物質の濃度uの変化は（4）の形の方程式で記述されるので，この方程式を拡散方程式とも呼ぶ。

振動・波動の問題

振動，または波動の現象では，時刻tにおける点xの変位u（t，x）があまり大きくないときは，それが時間tとともに変化する状態は次の方程式で記述される。

この形の方程式を双曲型方程式，または波動方程式という。

　（4）においてfが変数tを含まない場合で，温度が平衡状態にあるとき，すなわちuが時間とともに変化しないときは，\(\frac{∂u}{∂t}\)＝0であるから，（\(\frac{1}{c}\)）f（x）をあらためてf（x）と書けば，（4）は，

　Δu＝－f

となる。この形の方程式を楕円型方程式，またはポアソンの方程式という。とくにf≡0の場合の方程式Δu＝0は，ラプラスの方程式と呼ばれる。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

偏微分方程式
へんびぶんほうていしき
partial differential equation

2個以上の独立変数と未知関数およびその偏導関数の間の関係式を偏微分方程式という。関係式に含まれる偏導関数の最高階数をその方程式の階数という。未知関数とその各偏導関数について一次式であるような偏微分方程式は線形であるといわれ、そうでないとき非線形であるといわれる。また、最高階の偏導関数について一次式であるような偏微分方程式は準線形であるといわれる。独立変数がx、yのとき、一階準線形方程式は
　　a(x,y,u)u_x+b(x,y,u)u_y=c(x,y,u)（1）
と書くことができる。ここでuは未知関数で、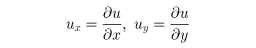

であり、a、b、cは既知関数である。同様に、二階線形方程式は
　　a(x,y)u_xx+2b(x,y)u_xy
　　　　+c(x,y)u_yy
　　　=d(x,y)u_x+e(x,y)_y
　　　　+f(x,y)u+g(x,y)　　　　　（2）
と書くことができる。ここでa、b、cなどは既知関数で、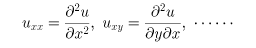

などである。偏微分方程式を恒等的に満たす関数をその方程式の解といい、偏微分方程式の解を求めることをその方程式を解くという。

　一階準線形方程式（1）を考える。x-y平面上の曲線P上の各点で与えられた関数に等しい（1）の解を求める問題を、（1）に対する一般初期値問題という。（1）に対し、x、y、uを未知関数とする連立常微分方程式
　　x′＝a(x,y,u),
　　y′＝b(x,y,u),
　　u′＝c(x,y,u)
を（1）の特性微分方程式といい、その解で与えられる（x,y,u）空間の曲線を（1）の特性曲線という。（1）の解が表す曲面u=u（x,y）は特性曲線により生成される曲面に等しい。したがって、特性曲線のx-y平面への射影が初期曲線Pに接しないで交わるならば、一般初期値問題の解はPの近傍で一意的に存在し、解は特性微分方程式を解くことにより得られる。かならずしも準線形とは限らない非線形一階偏微分方程式に対する一般初期値問題も、初期関数と初期曲線に対する適当な条件の下で、常微分方程式の初期値問題に帰着される。

　二階線形方程式（2）に対する一般初期値問題は、与えられた曲線P上の各点で与えられた関数に、その法線導関数を含めて等しくなるような解を求める問題である。

　いま、曲線Pの方程式を(x,y)=0とする。もし、
　　Q()≡a(x,y)x²+2b(x,y)_xy+c(x,y)_y²=0
が成り立つならばPを（2）の特性曲線といい、またつねにQ()≠0が成り立つならばPを非特性な曲線という。初期曲線、初期関数、係数関数a、b、cなどが解析的で、初期曲線が非特性ならばPの近傍で（2）の実解析的な解が一意的に存在する。これは高階非線形偏微分方程式に対しても成り立つ（コーシー‐コワレフスキーの定理）。

波動方程式u_xx-u_yy=0に対し、曲線y=0は非特性である。この場合、初期関数が解析的でなくとも解が存在し、解は初期関数に連続的に依存する。

ラプラスの方程式
　　u_xx+u_yy=0
に対し、y=0は非特性であるが、解は初期関数に連続的に依存しないし、また初期関数が解析的でないとき解が存在しないことがある。一般に偏微分方程式に対し付加条件を課して解を求める問題について、付加条件に対し解が一意的に存在して、さらに解が付加条件に連続的に依存するとき、この問題は適切であるといわれる。

　方程式（2）において「ac-b²＞0ならば楕円(だえん)型、ac-b²=0ならば放物型、ac-b²＜0ならば双曲型である」という。双曲型方程式に対しては初期値問題が適切である。楕円型方程式に対しては境界値問題が適切である。二階線形偏微分方程式は数理物理学において重要であり、詳しく調べられている。

［小林良和］

[参照項目] | 境界値問題 | 熱方程式 | 波動方程式 | ラプラス方程式

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

偏微分方程式
へんびぶんほうていしき
partial differential equation

未知関数が2個以上の変数の関数であって，未知関数のこれらに関する偏微分係数を含んでいる微分方程式を偏微分方程式という。たとえば，u を未知関数とすれば，
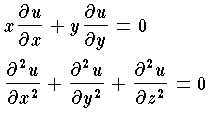などは偏微分方程式である。

出典　ブリタニカ国際大百科事典 小項目事典