翻訳|equation
精選版 日本国語大辞典 「方程式」の意味・読み・例文・類語
ほうてい‐しきハウテイ‥【方程式】
- 〘 名詞 〙 ( [英語] equation の訳語 )
- ① 未知数の値を求めるために、その満たすべき条件を等式の形に表わしたもの。未知数の値をその方程式の根(こん)または解といい、これを求めることを方程式を解くという。〔附音挿図英和字彙(1873)〕
- [初出の実例]「多角形に関する御存じの平均性理論によりますと、下の如く十二の方程式が立ちます」(出典:吾輩は猫である(1905‐06)〈夏目漱石〉三)
- ② 「かがくほうていしき(化学方程式)」の略。
- [初出の実例]「蒼鉛と珪酸ジルコニウムの化合物に関する方程式」(出典:機械(1930)〈横光利一〉)
改訂新版 世界大百科事典 「方程式」の意味・わかりやすい解説
方程式 (ほうていしき)
equation
x2+x-1=0や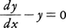 のように, 求めようとする数値や関数の条件が等式で表されたとき,その等式を方程式という。その等式の数は一つであるとは限らない。等式の数が複数であるときとくに連立方程式という。その数値や関数を求めることを方程式を解くといい,その数値や関数を方程式の解という。また解である数値や関数はこの方程式を満足するともいう。f(x)が文字xの多項式,分数式,無理式のとき,方程式f(x)=0はそれぞれ代数方程式,分数方程式,無理方程式といい,指数関数,対数関数,三角関数などを本質的に含む方程式は超越方程式と呼ばれる。
のように, 求めようとする数値や関数の条件が等式で表されたとき,その等式を方程式という。その等式の数は一つであるとは限らない。等式の数が複数であるときとくに連立方程式という。その数値や関数を求めることを方程式を解くといい,その数値や関数を方程式の解という。また解である数値や関数はこの方程式を満足するともいう。f(x)が文字xの多項式,分数式,無理式のとき,方程式f(x)=0はそれぞれ代数方程式,分数方程式,無理方程式といい,指数関数,対数関数,三角関数などを本質的に含む方程式は超越方程式と呼ばれる。
方程式x2+y2=2は文字x,yに関して無限個の解をもつが,x,yが整数であるような解は(x,y)=(1,±1),(-1,±1)の4個しかない。このように整数係数のn変数の多項式F1(x1,……,xn),F2(x1,……,xn),……,Fm(x1,……,xn)に対して,方程式F1(x1,……,xn)=0,F2(x1,……,xn)=0,……,Fm(x1,……,xn)=0の整数解のみを問題にするとき,不定方程式と呼び,整数解を求めることを不定方程式を解くという。不定方程式の解を求める一般的方法はなく,解がまったく存在しない場合,解が有限個存在する場合,解が無限個存在する場合の3通りがあるが,与えられた不定方程式の解がどの場合にあたるかを調べることも一般には困難な問題である。
解が関数であるような方程式は関数方程式と呼ばれる。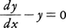 や
や 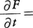
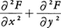 のように関数方程式に微分記号が入る場合は微分方程式と呼ばれる。さらに前者のように常微分しか出てこない場合を常微分方程式,後者のように偏微分が出てくる場合を偏微分方程式と呼ぶ。
のように関数方程式に微分記号が入る場合は微分方程式と呼ばれる。さらに前者のように常微分しか出てこない場合を常微分方程式,後者のように偏微分が出てくる場合を偏微分方程式と呼ぶ。 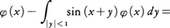 cos xのようにφを未知関数と考えて方程式の中に積分記号が出てくるものを積分方程式という。関数y(x)に対して⊿y(x)=y(x+1)-y(x)を差分,⊿2y(x)=⊿(⊿y(x))=y(x+2)-2y(x+1)+y(x)を第2階差分といい,⊿2y(x)-⊿y(x)=2y(x)のように差分が出てくる方程式を差分方程式という。また,f(x)+f(y)=f(x+y)のように微分や積分や差分をまったく含まない関数方程式もある。関数方程式を考えるときは,方程式に出てくる既知関数や求めるべき未知関数の定義域をはっきりさせておく必要がある。
cos xのようにφを未知関数と考えて方程式の中に積分記号が出てくるものを積分方程式という。関数y(x)に対して⊿y(x)=y(x+1)-y(x)を差分,⊿2y(x)=⊿(⊿y(x))=y(x+2)-2y(x+1)+y(x)を第2階差分といい,⊿2y(x)-⊿y(x)=2y(x)のように差分が出てくる方程式を差分方程式という。また,f(x)+f(y)=f(x+y)のように微分や積分や差分をまったく含まない関数方程式もある。関数方程式を考えるときは,方程式に出てくる既知関数や求めるべき未知関数の定義域をはっきりさせておく必要がある。
執筆者:上野 健爾
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「方程式」の意味・わかりやすい解説
方程式
ほうていしき
変数(いろいろな値をとりうる文字)を含んだ等式で恒等式(変数に任意の数を代入して成り立つ等式)でないものを方程式という。たとえば3x+1=x+5,2x-y=1などである。方程式の中の変数を未知数といい、それ以外の数字または文字、すなわち定数を既知数という。方程式はいわば式中の変数のとりうる値を条件づける等式である。論理的用語でいえば、方程式は命題関数である。未知数のとりうる値を解または根(こん)、すべての解の集合を解集合という。また解集合を求めることを方程式を解くという。同一解集合をもつ二つの方程式は同値であるという。方程式の一般的解法は順次同値な方程式に置き換え(同値変形)てなされる。
方程式の両辺が未知数についての整式であるものを整方程式といい、未知数の個数を元(げん)の数、未知数の最高次数を方程式の次数という。たとえばx2-2x+3=0は一元二次であり、2x3+y=3は二元三次である。複素数を係数にもつ一元n次方程式は複素数の範囲内で、ちょうどn個の解をもつ(方程式論の基本定理)。ただし重根はその重なった数だけ数えるものとする。整方程式の解を係数の代数式(四則と開法を有限回施した式)で表すことを、代数的解法という。五次以上の一般的な整方程式を代数的に解くことはできない(アーベルの定理)。
たとえば(a-b)x=a2-b2においてa=bのときは0x=0となり、解が無限個ある。このような場合に方程式は不定であるという。またax=1においてaがゼロのとき、解が存在しない。このようなとき方程式は不能であるという。
xとyの二元方程式、たとえばx-y+1=0の解は、xが任意の実数αをとるとき、yはα+1の値をとる。いまこの解を座標平面上の点(α,α+1)で表すと、このような点の集合は、y切片1、傾き1の直線となる。このとき、この直線を与えられた方程式のグラフという。一般に二元方程式f(x,y)=0のグラフは平面曲線となる。とくに二元二次方程式
ax2+bxy+cy2+ex+fy+g=0
のグラフは二次曲線(または円錐(えんすい)曲線)になる。つまり円、楕円(だえん)、放物線、双曲線および二直線のいずれかである。方程式のグラフは方程式の幾何学的解法に用いられる。
[竹内芳男]
百科事典マイペディア 「方程式」の意味・わかりやすい解説
方程式【ほうていしき】
→関連項目根
出典 株式会社平凡社百科事典マイペディアについて 情報
世界大百科事典(旧版)内の方程式の言及
【等式】より
…一方,(5),(6),(7)では,変数xやyに着目すると,xやyが特定の値をとるときにのみ等号が成り立つ。このような等式を方程式という。一般に,等式A=Bは次の性質をもつ。…
※「方程式」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

