被覆空間（読み）ひふくくうかん（英語表記）covering space

改訂新版　世界大百科事典

被覆空間 (ひふくくうかん)
covering space

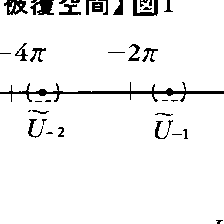
位相空間Xから位相空間Xへの連続写像p：X→Xがあって，Xの各点xに対し，xを含むXの開集合UとXの開集合族｛Ũ_λ;λ∈Λ｝が次の条件を満たすようにとれるとする。（1）pによってUのなかにうつるXの点はいずれかのŨ_λに含まれる。（2）各Ũ_λはpによってUの上に同相にうつる。（3）λ≠μならばŨ_λとŨ_μは交わらない。このときXはXの上の被覆空間であるといい，p：X→Xを被覆写像という。Xが連結ならば，Xの点xのとり方によらずp⁻¹（x）の個数は一定であるが，これが有限数nのとき，XはXをn重に被覆するという。例えば，数直線Rから半径1の円周Cへの写像pをp（t）＝（cost，sint）により定義すれば，すなわちRをCの上にのった無限に続いた〈ら線〉とみなせば，RはC上の被覆空間になる（図1）。また，nを自然数として，p：C→Cをp（cost，sint）＝（cosnt，sinnt）で定義すれば，CはCをn重に被覆する（図2）。被覆空間は数学の種々の分野で本質的な役割を演ずる。
執筆者：中岡 稔

図1～図2

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

被覆空間
ひふくくうかん
covering space

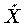リーマン面のときのように，空間 X を何重かに重ねて考える必要のあるとき，その重なったもの をつくり，射影 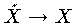で考える。この 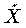を X の被覆空間という。

出典　ブリタニカ国際大百科事典 小項目事典