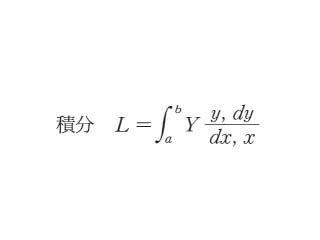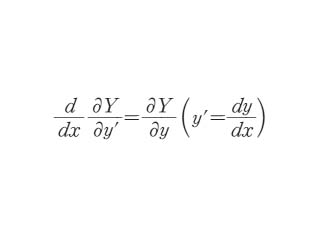世界大百科事典(旧版)内のオイラー‐ラグランジュの微分方程式の言及
【オイラーの方程式】より
…ここで関数z(x)の任意性により,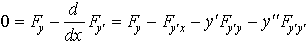 を得る。これをオイラーの方程式またはオイラー=ラグランジュの微分方程式という。この方程式は一般にyに関して2階の常微分方程式であるから,境界条件によって一つの解が定まる。…
を得る。これをオイラーの方程式またはオイラー=ラグランジュの微分方程式という。この方程式は一般にyに関して2階の常微分方程式であるから,境界条件によって一つの解が定まる。…
【変分法】より
…これを(3)に適用し,条件(2′)を使って部分積分を行うと,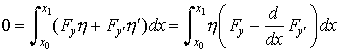 となるから,ηが(2′)を満たす関数の中では任意であることにより,
となるから,ηが(2′)を満たす関数の中では任意であることにより,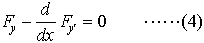 でなければならない。これをオイラー=ラグランジュの微分方程式,またはオイラーの方程式という。この方程式を満たす関数y(x)のうちで実際に(3)を最小にするものを求めればよい。…
でなければならない。これをオイラー=ラグランジュの微分方程式,またはオイラーの方程式という。この方程式を満たす関数y(x)のうちで実際に(3)を最小にするものを求めればよい。…
※「オイラー‐ラグランジュの微分方程式」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
1 花の咲くのを知らせる風。初春から初夏にかけて吹く風をいう。2 ⇒二十四番花信風...