ジョルダンの標準形（読み）じょるだんのひょうじゅんけい

日本大百科全書(ニッポニカ)

ジョルダンの標準形
じょるだんのひょうじゅんけい

逆行列の存在する行列を正則行列という。正方行列Aを正則行列Pを用いて変換する（P^-1APを求める）とき、いちばん簡潔に求められる方法はフランスの数学者ジョルダンがみいだしたジョルダンの標準形である。たとえば三次正方行列は次のいずれかの形にかならず変換される。

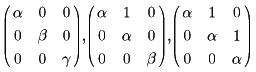
ただし、α、β、γはかならずしも相異なるとは限らない複素数（実数でもよい）である。

　一般的にいうと、まず、λを複素数（実数でもよい）とするとき、k次の行列J(λ, k)を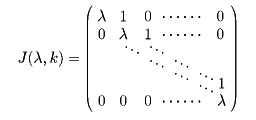

により定義する。いくつかのJ(λ, k)の形の行列を対角形に並べた行列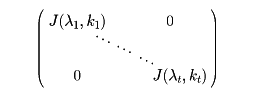

をジョルダン行列という。Aを正方行列とすればP^-1APがジョルダン行列となる正則行列Pがかならず存在する。Aのジョルダン行列はAによって一意的に定まる。

［足立恒雄］

[参照項目] | 行列

出典　小学館　日本大百科全書(ニッポニカ)