実数（読み）ジッスウ（英語表記）real number

デジタル大辞泉

じっ‐すう【実数】

１ 実際の数。「参加者の実数を調べる」
２ 有理数と無理数の総称。→虚数
[類語]正味

出典　小学館

精選版 日本国語大辞典

じっ‐すう【実数】

1. 〘 名詞 〙
2. ① 実際に存在する数量。予測した数量や粉飾した数量に対していう。
   1. [初出の実例]「五と云へども掛一をのけて実数は四ぞ」(出典：史記抄（1477）一八)
3. ② 有理数と無理数の総称。⇔虚数。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕
4. ③ コンピュータの中で使用される数のうちで、小数点のついている型の数をいう。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

実数
じっすう
real number

有理数と無理数をあわせて実数という。有理数には、自然数（正の整数）、0、負の整数が含まれる。実数とはなんであるか、それがどのような性質をもつかについての本格的研究は、19世紀中ごろからワイアシュトラース、デーデキント、メレー、カントルによって相次いで展開された。

［竹之内脩］

実数概念の変遷

古代ギリシアでは、二つの量がともにある別の量の整数倍となっている場合をおもに考え、そうでない場合は不通約量として敬遠した。その後、不通約量も含めて一般に数とは、二つの線分の長さの比のことであるという考え方がとられた。十進記数法は、インド、アラビアにおいてつくられ、12世紀ごろからヨーロッパに輸入されたが、それは整数を表すためのものであった。今日の小数記法が考案されたのは16世紀なかば、ステビンによってであった。この記法の発見により、その後、無限小数という概念が生じたことと思われる。17世紀前半、デカルトは、直線に1点Oと単位点Eを与え、OEを単位として長さを測ることにより、数と直線上の点の1対1の対応関係を確立した。

　コーシーは、1830年、数列a₁, a₂,……がある極限値に収束するならば、互いの項の差|a_n－a_m|は、n、mが大きくなっていくときいくらでも小さくなることを述べ、逆に、そのような性質をもった数列は収束することを主張した。これを出発点として厳密に公理的に構成したならば、現代的な意味での実数概念に接近したであろうが、コーシーは単にこれを主張したにとどまった。ボルツァーノも1851年の書物のなかで実数の認識に関する議論を展開している。

［竹之内脩］

実数概念の確立

デーデキントは1872年に、有理数から出発して実数をつくりあげる議論を展開した。彼は、直線上の点と数との間の対応に注目し、直線は、それをどの点で切っても同じ状態（いずれか一方の半直線は端点をもち他方にはない）になるので、それが実数の本質だと考えた。そして有理数だけでは、それをあるところで切断するとき、同じ状態にならないので、むしろこの切断自体を実数の本質と把握するのが妥当であるとした。詳しく述べると次のようである。

　いま、有理数の全体Qを、次のような二つの集合A、Bに分割する。(1)A、Bは共通な要素をもたない。そして両方をあわせるとQ全体になる。(2)Aに属する数a、Bに属する数bをとると、いつでもa＜bである。このとき、このA、Bの組みを一つの有理数の切断といい、これを(A－B)で表す。そして、Aをこの切断の下組、Bを上組という。このとき次の三つのケースがおこる。

〔1〕Aに最大の数があり、Bには最小の数がない。

〔2〕Aには最大の数がなく、Bに最小の数がある。

〔3〕Aには最大の数がなく、Bには最小の数がない。

　第一、第二のケースでは、Aの最大数、あるいはBの最小数がこの切断に対応するとすれば、これは一つの有理数を表しているものとみることができる。第三のケースは、これがちょうど無理数に対応しているものと考えられる。デーデキントは、このように切断の全体を考え、その間に演算を定めることによって、これを実数の体系として把握することができるとしたのである。

　メレーは1869年に著した書物のなかで、カントルは1872年の論文で、コーシーの立場を継承した実数論を展開した。すなわち、数列a₁, a₂,……は、既述のコーシーのいう性質をもつとき、基本列あるいはコーシー列という。有理数の範囲で考えると、基本列は収束するとは限らない。そこで、有理数からなる基本列を考え、この列そのものが一つの数を定めると考える。二つの基本列a₁, a₂,……, a₁′, a₂′,……に対して、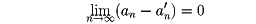

であるとき、この二つの基本列は同じ数を定めるものとすれば、このように基本列で定められる数のうち異なったものの全体によって、実数の体系がつくられる、とするのである。この考え方は適用の範囲が広く、数学のいろいろな分野で完備化として知られる。

　ヒルベルトは1899年、幾何学基礎論を研究した際、実数の体系の公理的構成を考えた。それは四則演算に関する一般的性質、大小に関する一般的な性質と、アルキメデスの公理（任意の正の数α、βをとるとき、αを次々と加えていくといつかはβより大きくなる）をあげ、このような体系のうちで、それ以上大きくできないものが実数の体系だとした。この、これ以上大きくできないという性質を完全性というが、これは、たとえば、(1)切断はつねに下組に最大数があるか、上組に最小数があるかである。(2)基本列はかならず収束する。(3)上に有界な集合は、かならず最小の上界、すなわち上限をもつ、などと同値である。そして、このようにして実数を公理論的な立場でとらえうる、としたのである。

　ヒルベルトは、数学の体系の厳格な基礎づけを目標として数学基礎論を創始したが、その大きな目標の一つは、実数の体系に対して明確な基礎を与えることであった。これはまだ将来の大きな問題として残されている。集合論を創始したカントルは、基数の大きさの順序として、可算基数ℵ₀（アレフ・ゼロと読む）の次の大きさの基数は、実数の基数であろうと考えた。これを連続体仮説という。これはカントル以来、大きな問題であったが、近年、この連続体仮説は従来の集合論の公理系とは独立なものであることが知られた。

［竹之内脩］

『竹之内脩著『集合・位相』（1970・筑摩書房）』▽『高木貞治著『数の概念』（1949・岩波書店）』

[参照項目] | 複素数

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

実数
じっすう
real number

無理数と有理数を合わせて実数という。分数で表される有理数は古代から知られていたが，近代になって小数で近似することによって，無理数も無限小数で表されるようになった。そこで，有理数ないしは有限小数の極限として実数が考えられ，数直線として，実数空間の点のように考えられるようになった。19世紀になって，正式に実数論として論じられるようになるが，近似の幅をせばめて，コーシー列の極限として定義するゲオルク・F.L.P.カントルの実数論と，半直線の端として定義するユリウス・W.R.デデキントの実数論とが有名である。ほかにも多くの構成法が知られているが，今日よく用いられるのは，次のデデキントの方法である。大きさに従って順序のつけられた有理数全体を，次のような二つの組 R₁，R₂に分割することを，有理数域における切断という。(1) R₁，R₂は，いずれも空でない（すなわち少なくとも一つの有理数を含む）。(2) R₁の各数は，R₂のどの数よりも小さい（デデキントの切断）。この切断を，記号 (R₁，R₂) で表すことにする。これには，次の三つの場合が可能である。
(1) R₁に最大数があり，R₂に最小数がない。
(2) R₁に最大数がなく，R₂に最小数がある。
(3) R₁に最大数がなく，R₂に最小数がない。
以上のうち，(1)と (2)を合わせて第1種の切断といい，(3)を第2種の切断という。デデキントは，第1種の切断における R₁の最大数または R₂の最小数を有理数，第2種の切断を無理数と定義した。実数（デデキントの意味で）とは，このような切断 (R₁，R₂) の全体をさしていう。

出典　ブリタニカ国際大百科事典 小項目事典

改訂新版　世界大百科事典

実数 (じっすう)
real number

数直線上の各点に対応していると考えられる数であるが，19世紀になってこのような素朴なとらえ方では不十分であることがわかり，主として解析学における必要から実数の正確な定義を与えることが考えられた。J.W.R.デデキントは切断という考えを用いて，またG.カントルは基本列という考えを用いて実数の正確な定義を与えた。

　実数は分数の形で表される有理数と，分数の形で表されない無理数とに分けられる。また，有限または無限小数による表示もでき，有理数からなる数列の極限としても表せる。実数αの絶対値は，αが0または正の数のときにはα，負の数のときには－αと定義され，｜α｜で表す。絶対値には次の性質がある。（1）｜α｜≧0，（2）｜α＋β｜≦｜α｜＋｜β｜，（3）｜α｜＝0⇔α＝0。

　α，βが実数ならば，α±β，αβ，α/β（β≠0）も実数であり，実数においては有理数と同様に四則演算ができる。実数が有理数と異なる点は，実数は連続的であることである。これは次のように述べられる。実数全体を次の条件をもつ二つの集合A，Bに分ける。（1）A，Bは空でない。（2）Aの各元はBの各元よりも小さい。このように実数を分けると，（1）Aの元で最大のものがあるか，または，（2）Bの元の中に最小のものが存在する。またアルキメデスの公理Archimedes' axiomと呼ばれる次の性質がある。〈α，βが正の実数であれば，nβ＞αとなる自然数nが存在する〉。他方，数列の極限の考えは，微分積分学では基本的である。
執筆者：斎藤 裕

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

実数【じっすう】

有理数と無理数を合わせたもの。デデキントによれば，有理数全体を二つの組A，Bに分け，Aに属する各数はBに属する各数より小さくなるようにした（切断）とき，1.Aに最大数があり，Bに最小数がない，2.Aに最大数がなく，Bに最小数がある，3.Aに最大数がなく，Bに最小数がない，の三つの場合を生ずるが，1.の最大数と2.の最小数を有理数とし，3.の場合を無理数と定義する。これにより，有理数に無理数を加えた実数は連続性をもち，一つの直線上の点の全体と１対１に対応（１対１対応）する。→数

出典　株式会社平凡社

世界大百科事典（旧版）内の実数の言及

【数】より

…〈かず〉ともいう。数学で単に数という場合，複素数を意味するが，もっと狭く，実数に限定した意味に用いられることもよくある。おおまかに分類すれば次のようになる。…

※「実数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」