フェルマー数（読み）フェルマーすう（その他表記）Fermat number

改訂新版　世界大百科事典

フェルマー数 (フェルマーすう)
Fermat number

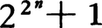の形の整数をフェルマー数といい，とくに素数のときフェルマー素数という。以下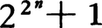，をF_nと記す。F₀＝3，F₁＝5，F₂＝17，F₃＝257，F₄＝65537で，これらはすべて素数であることにP.deフェルマーが気づき，さらにF_nはすべて素数であろうと予想したことによりこの名がある。フェルマーはまた　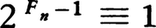（modF_n）が成立することも示した。1732年にL.オイラーはF₅＝641×6700417と分解し，F₅が合成数であることを発見した。彼はF_nの素因数をpとすると，p≡1 （mod 2ⁿ⁺¹）であることを見いだし，これを使ってF₅の素因数641を見いだした。さらにルカスE.Lucasはn≧2のとき，F_nの素因数pに対してp≡1（mod 2ⁿ⁺²）であることを見いだし，これを使ってF₁₂の素因数7×2¹⁴＋1を発見した。またF_nが素数であるための必要十分条件は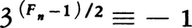（mod F_n）であることも知られている（プパンP.T.Pepinの判定法）。n≧5のときF_nが素数である例は知られていない。
執筆者：上野 健爾

出典　株式会社平凡社「改訂新版　世界大百科事典」