素数（読み）ソスウ（英語表記）prime number

デジタル大辞泉

そ‐すう【素数】

1とその数以外に約数がない、1を除く正の整数。2・3・5・7…など無限にある。→合成数
[補説]100までの素数は、2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97。25個ある。

出典　小学館

共同通信ニュース用語解説

素数

2以上の自然数で、1とその数以外では割り切れない数。無限にある。自然数を素数の積で表すことを素因数分解といい、例えば60は2と3と5の積に分解できる。大きな素数をかけた数ほど素因数分解が難しくなるため、ITの世界では「素因数分解できたら鍵が開く」という仕組みの暗号に使われる。10349は二つの素数131と79の積だが、手計算だとすぐには分からない。これも計算機では簡単に判明するため、暗号にはもっと大きな桁の数が用いられる。極めて大きな素数を見つけ出す競争も行われ、これまでに1742万5170桁の素数が発見されている。

更新日:2014年2月26日

出典　共同通信社 共同通信ニュース用語解説

精選版 日本国語大辞典

そ‐すう【素数】

1. 〘 名詞 〙 １より大きい整数で、１とその数自身以外に約数をもたないようなもの。２、３、５、７など。⇔合成数。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

素数
そすう
prime number

1と自分自身以外に約数をもたない自然数のうち1でないものを素数という。自然数aが自然数bを割り切ることをa|bという記号で表す。1でない自然数pが素数であることはまた、自然数a、bに対してp|abならば、p|aまたはp|bが成り立つ、ともいいかえられる。

　ユークリッドの『ストイケイア』のなかに、素数は無数に存在することが証明されている。その証明を現代風に述べてみる。2、3、5、……、pがすべての素数であるとし、N=(2・3・5・……・p)+1という数を考える。Nは2、3、5、……、pのいずれによっても割り切れない。したがって1と自分自身以外に約数をもたないのでNは素数である。Nは2、3、5、……、pのどれにも一致しないから、それらがすべての素数であるという仮定に反する。したがって素数の数は有限ではない。

　素数表をつくるには「エラトステネスのふるい」と称する方法を用いる。現代でも基本的にはこの方法を改良して素数表をつくる。最初に2から順に自然数を並べる。まず2を残し、2の倍数を消していく。次に残った数のなかで最小の数3を残し、3の倍数を消していく。次に残った数のなかで最小の数5を残し、5の倍数を消していく。以下同様に続けて素数表を得る。なおエラトステネスは紀元前3世紀ごろのギリシアの天文学者・地理学者である。

　2以上の自然数は素数の積として表せる。またその表し方は順序を除けば一意的である。たとえば12は3×2×2と素因数分解される。それ以外にも2×2×3,2×3×2と素因数分解が考えられるが、これらはすべて因数の順序を入れ換えれば同一の分解となる。素因数分解とその一意性についてはユークリッドの『ストイケイア』に記述があるが、その重要性は、ガウスの『数論研究』Disquisitiones Arithmeticae（1801）に至るまで十分認識されなかった。その重要性は、複素数にまで整数の概念を拡張するとき、かならずしも素因数分解とその一意性が成り立たないことによって逆に認識される。

　11と13、17と19のように差が2の素数の組を双子素数という。双子素数は無数に存在するという予想があるが、現在未解決の問題である。

［足立恒雄］

算術級数の定理

たとえば一位の数が1である素数としては11,31,41,61,71などがある。また一位の数が3である素数としては3,13,23,43,53,73,83などがある。はたしてこれらの素数はそれぞれ無数にあるだろうか。このような素数の無限性を精密にした疑問に答えるのが算術級数の定理であって、1837年ディリクレによって初めて正確に証明された。

　いま、a、dを互いに素な自然数とする。等差数列a,a+d,a+2d,……,a+nd,……のなかには無数に素数が存在する。たとえばaを1、dを10とすれば、一位の数が1である素数が無数に存在することを意味する。証明は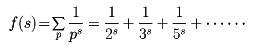

という素数のすべてにわたる和の級数に関する性質を用いて行われる。とくにsが1に近づくときf(s)は発散する。このことから素数が無数にあることがわかる。なぜなら、有限個ならばf(s)はいつでも確定するはずだからである。

　算術級数の定理は単なる興味を超えた、基本的定理である。同じことが一次以上の多項式についていえるかは、まったく未知の問題である。たとえば
　　n²+1　（nは自然数）
の形の素数が無数にあるかどうか、いまだにわかっていない。

［足立恒雄］

素数分布

自然数xを超えない素数の個数をπ(x)で表す。たとえば
　　π(2)=1,　 π(10)=4,
　　π(100)=25,π(1000)=168
である。アダマールとド・ラ・バレ・プーサンは1896年独立に素数定理、すなわち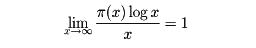

が成り立つことを証明した。したがって大きなxについてはπ(x)はほぼx/logxに等しい。たとえばx=10⁷のとき
　　π(x)=664579,
　　x/logx=620417
である。

　素数のように不規則に分布するものがx/logxという簡単な関数によって近似され、しかも、それが証明されるというのは驚くべきことであろう。初期の証明には関数論の深い結果が用いられたが、セルバーグによって関数論を用いない証明が得られている（1949）。

［足立恒雄］

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

素数 (そすう)
prime number

1よりも大きい自然数で，1と自分自身以外に約数をもたないもの。例えば，2，3，5，7，11などである。2以外の素数は奇数なので奇素数という。1以外の自然数で素数でないものおよびそれにマイナスの符号をつけたもの（±4，±6など）を合成数という。与えられた自然数nが素数かどうかを判定するには\(\sqrt{n}\)以下の素数で割れるかどうか調べてみればよい。\(\sqrt{n}\)以下の数が素数かどうかわからなければそれでも割ってみる。しかし大きな自然数が素数かどうかを判定するのは一般に容易でない。自然数の中から素数を選び出すエラトステネスのふるいと呼ばれる方法が知られている。素数の判定が容易でないため，大きい素数を見つけることが興味を引いてきた。とくにメルセンヌ数と呼ばれる素数を見つけるのには便利な方法があって，コンピューターを用いて次々に大きな素数が見いだされている。特別な形の素数としてフェルマー数というのがある。

　素数についての研究は古代ギリシア時代までさかのぼる。ユークリッドは《ストイケイア》の中で素数に関する次の重要な定理を述べている。（1）1以外の自然数はすべて素数の積として一意的に表される。（2）素数は無限に存在する。（2）は次のようにして示される。p₁，……，p_nがすべての素数であったとしよう。p₁……p_n＋1を割る素数の一つをpとすれば，これはp₁，……，p_nとは明らかに異なる。これは矛盾である。しかしその後長い間この方面の研究は進展を見なかった。19世紀になってC.F.ガウスは素数の分布，すなわちどのような規則に従って素数が自然数の中に現れるかという問題を考察した。素数の分布はたいへん複雑である。素数pの次の素数はどのくらいの大きさであろうか。これについては，pの次の素数は2pよりも小さい（チェビシェフの定理）という程度のことしかいえない。実際，100！＋2，100！＋3，……，100！＋100（！は階乗）はすべて合成数で，このように素数を含まないいくらでも長い区間を作ることができる。一方，3と5，5と7のように2だけ違う素数の対を双子素数という。2は，2と3の場合を除けば素数の間隔としては最小のものであるが，このような素数の組は無限に存在することが予想されている。このように，個々の素数は非常に不規則に分布しているのだが，ガウスはx以下の素数の個数は約log xであるという素数定理を見いだした。P.G.L.ディリクレも，aとmが互いに素な自然数とすると，等差数列，a，a＋m，a＋2m，……の中に素数が無限個現れるという算術級数の定理と呼ばれる結果を示した。このような素数分布に関する研究が，その後の解析的整数論の発展を促した。
執筆者：斎藤 裕

図－エラトステネスのふるい

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

素数
そすう
prime

1より大きい整数 p が，1と p 以外には約数をもたないとき，p を素数という。たとえば 2，3，5，7，11，13，17，19，23，…はみな素数である。素数でない任意の自然数は，一意的に素因数分解できる。自然数 n が素数であるかどうかは，2≦p≦√n の範囲にあるすべての素数 p で n を割って，割り切れるかどうかで判断できる。すなわち，割り切れなければ n は素数，割り切れれば n は合成数であると判断する。エラトステネスのふるいも本質的には，これと同じ原理によって素数を判定している。またメルセンヌ素数も素数の有力な判断法を提供している。素数が自然数のなかにどのように分布しているかについての研究は，整数論の重要な一部分で，素数分布論という分科もある。素数は古代から認識されており，ユークリッドは素数が無限に存在することの証明を行なっている。20世紀になってコンピュータを用いることで 200万桁を上回る素数が確認されている。

出典　ブリタニカ国際大百科事典 小項目事典

知恵蔵

素数

1と自分自身以外では割り切れない自然数。2、3、5、7、11、13、17、19……と続き、無限個存在することが、古代ギリシャでユークリッドによって示されていた。「3と5」、「5と7」、「11と13」のように、偶数の両隣の組になっている素数を双子(ふたご)素数という。双子素数は無限個あると予想されているが、未解決である。知られている最大の双子素数は2003663613×(2の195000乗)±1(2007年9月現在)。また、4以上の偶数は2つの素数の和として書けるという予想(ゴールドバッハの予想: Goldbach conjecture)も未解決。4=2+2、6=3+3、8=3+5など。大きな素数は公開鍵暗号に利用されている。コンピューターを使い大きな素数を発見する研究が行われており、2006年9月に発見された2(2の32582657乗)-1が、現在具体的に知られている最大の素数。その桁数は約981万桁(けた)。このように、(2のn乗)-1の形の素数はメルセンヌ(Mersenne)素数と呼ばれ、07年9月末現在、素数になるnが計44個知られている。素数の分布はリーマンのゼータ関数(リーマン予想)と関係している。ある自然数が素数であるかどうかを判定することは実用上重要であるが、02年にアグラワル(M.Agrawal)、カヤル(N.Kayal)、サクセナ(N.Saxena)の3人のインド人研究者によって、多項式時間で判定できるという驚くべき結果が得られた。

(桂利行 東京大学大学院教授 ／ 2008年)

出典　(株)朝日新聞出版発行「知恵蔵」

百科事典マイペディア

素数【そすう】

１より大きい整数のうち，１とそれ自身以外に約数をもたないもの。たとえば２，３，５，７，11など。素数は無限に多く存在する。任意の自然数は素数のべきの積として一意的に表される（素因数分解）。自然数の中から素数を発見するにはエラトステネスの篩(ふるい)と呼ばれる方法がある。
→関連項目自然数｜リーマン予想

出典　株式会社平凡社

世界大百科事典（旧版）内の素数の言及

【整数論】より

…r＝0であるとき，aはbで整除される，または割り切れるといい，aはbの倍数，bはaの約数であるという。
［素数］
　1以外の正の整数pで，1と自分自身以外に正の約数をもたないものを素数という。2以外の素数は奇数なので奇素数という。…

※「素数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」