フェルマー
ふぇるまー
Pierre de Fermat
(1601―1665)
フランスの数学者、政治家。トゥールーズの近く、ボーモン・ド・ロマーニュに生まれる。父は生地の副領事で皮革商であった。フェルマーはトゥールーズの大学で法律を学び、1631年5月トゥールーズの参事官となって政治家としての第一歩を踏み出した。その後1648年にはトゥールーズ議会の議員となり、生涯をその地で送った。ここは政治的に安定しており、職務の余暇に古い数学書を読みながら数学を研究し、その研究成果を、交際のある当代の代表的な数学者に手紙で知らせていた。自分の成果を論文や著作の形で公表することを好まなかったらしく、高く評価される彼の研究の多くは、その死後、1679年にまとめて発表された。
フェルマーは、デカルトとは独立に、曲線y=f(x)を横座標xに応じて、長さyの線分をとりながら、直線や円錐(えんすい)曲線がそれぞれ一次、二次の方程式で与えられることを示した。この仕事は今日の解析幾何学の基礎を与えるものである。さらに極小を求める方法として、極限をとる考えはなかったが、
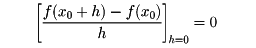
を解いて極値x0を求め、極大・極小を出した。これは今日pseudo-equality methodとよばれている。この方法を用いて、曲線に接線を引くことができた。またフェルマーはパスカルとの間で、さいころ賭博(とばく)を途中でやめたとき、賭(か)け金をどのように分配するかについて文通で論じた。これは確率論の問題を扱ったもので、フェルマーは確率論の創始者の一人でもある。
フェルマーの名を不朽にしたのは、彼の数論の研究であった。古代ギリシアのディオファントスの『算数論』のラテン語訳書を読み自分の出した結果をこれに書き込んだ。pが素数で、aとpが互いに素であればap-1-1はpで割り切れる。4n+1の形の素数は二つの平方数の和として一通りに書ける、そして立方数を二つの立方数に、また四乗数を二つの四乗数に、一般に2より大きいべき数を二つの同じべき数に分けることはできない、などである。初めの二つは証明できるが、最後のものは、xn+yn=znの整数解を求める問題で、長い間、完全に解けていなかった。これは「フェルマーの予想」または「フェルマーの問題」とよばれている(この問題については、1994年にワイルズAndrew J. Wiles(1953― )によって証明が完成されている)。数論の結果の証明に、数学的帰納法の一つの変形である無限降下法をしばしば利用した。フェルマーは22n+1はどんな自然数についても素数であると予想したが、n=5のとき641×6700417となり、素数ではない。この形の数22n+1は今日フェルマー数とよばれている。フェルマーの予想とは違って、今日では、n≧5のときフェルマー数は素数ではないと考えられている。
[井関清志]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
フェルマー
Pierre de Fermat
生没年:1601-66
フランスの数学者。トゥールーズに近いボーモン・ド・ロマーニュの富裕な商家に生まれ,ボルドーで法学を修めてトゥールーズの裁判所顧問となり,一生をその地方に過ごした。余暇に数学を研究し,得られた結果を知人への手紙や手記に書き残した。F.ビエトの代数学に通じ,R.デカルトのように著書で公表はしなかったけれども解析幾何学の方法を得ていた。微積分学についての先駆的創見もあり,確率論の端緒となった問題に関するB.パスカルとの文通もある。古典語にも詳しく,ディオファントスの《数論》に多くの注を加えた。その欄外に〈n≧3のときxn+yn=znの整数解はないことの驚くべき証明を得た〉という意味のことを記したのはことに有名である(フェルマーの大定理)。数論についてはそのほかにも多くの著しい発見がある。幾何光学上のフェルマーの原理も知られている。彼の業績は長男サミュエルSamuelがまとめ,19世紀末になってP.タンヌリらが整理公刊した。
執筆者:弥永 昌吉
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
フェルマー
フランスの数学者。1631年トゥールーズ地方議会の議員となり,余暇に数学を研究。成果はデカルトやメルセンヌへの手紙などに記しただけで公表せず,他の手記は1679年子が公刊。ディオファントスの数論の訳書に刺激されて数論を研究,余白にフェルマーの定理の書込みがあり,近代整数論の端緒を開いた。円錐曲線の研究から解析幾何学を考案,微積分の先駆的研究もある。光線の通路に関するフェルマーの原理も有名。
→関連項目解析幾何学
出典 株式会社平凡社百科事典マイペディアについて 情報
Sponserd by 
世界大百科事典(旧版)内のフェルマーの言及
【解析幾何学】より
…この際,数や代数学は用いられず,もっぱら図形が使用される。他の方法はP.deフェルマーやR.デカルトによって案出された方法で,平面や空間に座標を導入して,図形を数の間の関係によって表し,また逆に数の間の関係を図形で表現して,図形の問題を数の問題に翻訳し,代数の計算によって幾何の問題を処理するというものである。前者を総合幾何学または純粋幾何学というのに対し,後者を解析幾何学という。…
【数学】より
…代数計算によって,数学理論を構成するのは,そこから始まったのである。P.deフェルマーは,代数的方法を駆使して,ディオファントスの数論を発展させ,また曲線の接線を求めることや,最大最小の問題を扱い,光学にも応用した。またB.パスカルとの往復書簡では確率論の先駆となった問題を論じた。…
【整数論】より
…このとき,pと互いに素な整数aに対して, ap-1≡1 (mod p)が成り立つ。これはフェルマーの定理と呼ばれている。p-1より小さい正の整数kに対しては,akと1がpを法として合同にならないとき,aはpを法としての原始根,またはpの原始根という。…
【魔方陣】より
…立体方陣も平面の場合と同様に,対称,相結などが考えられる。立体四方陣はP.deフェルマーが最初に作ったが,4本の立体対角線の成立するものは久留島義太が初めて作った。
【歴史】
中近東でもっとも古い方陣を集めたものに,989年ころのイスラムの百科事典がある。…
※「フェルマー」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by