ヘッセの標準形（読み）へっせのひょうじゅんけい（英語表記）Hesse's normal form

日本大百科全書(ニッポニカ)

ヘッセの標準形
へっせのひょうじゅんけい
Hesse's normal form

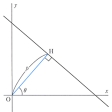
直線または平面の方程式の一つの特殊な形。平面上で一つの直線に原点Oから垂線を下ろし、垂線OHがx軸となす角をθ(0≦θ＜360゜)、またOH=p(≧0)とすれば、この直線の方程式は
　（＊）　　xcosθ+ysinθ=p
となる。ここで、x、yは直交座標とする。（＊）を直線のヘッセの標準形という。一般に、平面上の直線の方程式は
　　ax+by+c=0 (a²+b²≠0)
の形である。両辺を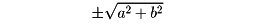

で割れば、
　（＊＊）　　lx+my=n(≧0), l²+m²=1
の形となる。したがってl=cosθ,m=sinθとなる角θがみつかるので、（＊＊）もヘッセの標準形である。ヘッセの標準形の利点は、平面上の任意の点(x₀,y₀)から直線（＊＊）に下ろした垂線の長さが|lx₀+my₀-n|で与えられ、簡単に求められることである。空間では、平面の方程式のヘッセの標準形がある。

［立花俊一］

ヘッセの標準形

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

ヘッセの標準形
ヘッセのひょうじゅんけい
Hesse's normal form

直交軸の設定された平面上の直線の方程式は，原点Oからこれにおろした垂線 OH の長さを p(p≧0) ，OH が x 軸の正の向きとなす角を θ とすれば x cos θ＋y sin θ＝p の形に書かれる。この直線の方程式をヘッセの標準形または法線形という。ヘッセの標準形は，直交軸の設定された空間の平面の方程式に対しても拡張される。

出典　ブリタニカ国際大百科事典 小項目事典