直線（読み）チョクセン

デジタル大辞泉

ちょく‐せん【直線】

１ まっすぐな線。「直線コース」
２ 数学で、異なる2点を通り、同一方向に無限にのびる線。→半直線 →線分
[類語]一直線・線・ライン・筋すじ・弧・罫・線条・曲線・実線・破線・点線・波線・斜線・アンダーライン・傍線・折れ線・垂線・鉛直線・接線・水平線・平行線・対角線・双曲線・放物線・母線・螺線らせん・割線・中線・中心線

出典　小学館

精選版 日本国語大辞典

ちょく‐せん【直線】

1. 〘 名詞 〙
2. ① まっすぐな線。また、まっすぐな方向。
   1. [初出の実例]「方形は四箇の直線にて成り」(出典：暦象新書（1798‐1802）中)
3. ② 数学で、線のうち、その上のどの二点に対しても、それらの間の最短路となっているようなもの。ふつう、両方に限りなくのびているものをさす。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

直線 (ちょくせん)
straight line

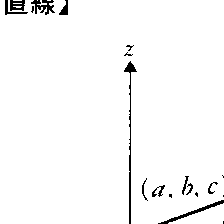
直線は引っ張られた糸や光線からの抽象として得られた概念で，字義どおりまっすぐな線のことであるが，数学で直線というときは両側に限りなく延びていることを要請し，有限なものを線分，一方の側だけに限りなく延びたものを半直線と呼んで区別している。ユークリッドは〈直線はその上の点に対して一様に横たわる線である〉といって直線の説明をしているが，直線のような原始概念を定義できるはずもないので，現今の数学ではD.ヒルベルトに従って直線は無定義な数学的対象物とし，それの数学的に表現できる性質を公理として与え，これを直線の根拠にしている。なお，解析的には，定数a，b，c，l，m，n（l²＋m²＋n²≠0）を用いて，

　x＝a＋lt，y＝b＋mt，z＝c＋nt　（tは実数）　

の形に表される（x，y，z）を座標にもつ点の集合が直線であるということができる（図）。
執筆者：中岡 稔

図－直線

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

直線
ちょくせん
line

ユークリッド幾何学における直線とは，幅はもたず，両側の方向に無限に延びたまっすぐな線である。両端をもち，長さが有限なまっすぐな線は線分と呼ばれる。また，一つの端点から一方向に無限に延びたまっすぐな線を半直線という。座標平面における直線は a，b，c を定数として，一次式 ax＋by＝c で表される。ユークリッドの『原本』においては，点と直線は無定義述語であり，これらの満たす性質を公理，公準として仮定し，それを出発点として論理を展開した。ここで仮定された重要な性質として次の二つがある。(1) 異なる二つの点を通る直線はただ一つ存在する。(2) 一つの直線 Lとその上にない一点に対して，この点を通って Lに平行な直線がただ一つ存在する。19世紀にニコライ・ロバチェフスキーとヤーノシュ・ボーヤイによって，非ユークリッド幾何学が発見され，平行線に関する上の性質 (2)を満たさないが，ユークリッドの『原本』の他の公理を満たす幾何学の体系が存在することが明らかになった。

出典　ブリタニカ国際大百科事典 小項目事典

日本大百科全書(ニッポニカ)

直線
ちょくせん

糸をぴんと引っ張ってできるようなまっすぐな線が直線である。といっても、直線そのものを定義することはできない。異なる2点で一つの直線が定まる、あるいは、二つの平面の交線である、などというように他の図形との相互関係によって直線が規定される。「線には長さはあるが幅も厚みもない」。また、「線が動いて面となる」など一見矛盾した説明もなされるが、幾何を公理的に構成するときは、点と直線と平面とは、いわゆる無定義述語であり、それらの相互関係が公理として述べられる。図形の性質を考えていくときは、定木(じょうぎ)に従って線を引いて、理想化された直線の表現として考えていく。異なる2点でただ一つの直線が定まる。直線上の1点によって直線は二つの部分に分けられ、それぞれを、その点を端点とする半直線という。直線上の異なる2点をとるとき、2点の間にある直線の部分をその2点を端点とする線分という。平面上の2点でできる直線上の点はすべてその平面上にある。平面はその直線によって二つの部分に分けられ、それぞれをその直線を境界線とする半平面という。同じ半平面上の2点を結ぶ線分は境界線と共有点はなく、異なる半平面上それぞれに点をとって結ぶと、境界線とかならず共有点がある。平面上の二直線については、共有点がないか（平行）、共有点がただ一つか（交わる）、あるいは完全に一致してしまう。空間の二直線が同一平面上にないとき、ねじれの位置にあるという。

［柴田敏男］

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

直線【ちょくせん】

常識的にはまっすぐな線，２点間の最短距離を与える線などというが，厳密な定義ではない。ユークリッド空間，アフィン空間，射影空間では一次元の部分空間をいう。n次元ユークリッド空間における直線の解析的定義は，tをパラメーターとする方程式x(/i)＝a(/i)＋b(/i)t（i＝１，２，…，n，−∞＜t＜∞，a(/i)，b(/i)は定数）をみたす点（x₁，x₂，…，x(/n)）の全体が作る集合。→曲線
→関連項目線｜線分

出典　株式会社平凡社

デジタル大辞泉プラス

直線

英国の作家ディック・フランシスのミステリー（1989）。原題《Straight》。競馬界を舞台にしたシリーズの第28作。

出典　小学館

世界大百科事典（旧版）内の直線の言及

【ヤントラ】より

…　図形としては，次のようなものが用いられる。点(それ以上凝縮しえない究極的相を示す)，直線(成長･展開の相を示す)，円(〈全体〉を表す)，四角形(自然の質料を表す)，三角形(サーンキヤ学派の説く純質･激質･暗質という自然の三つの性質などを示し，下向きのものは女性原理を，上向きのものは男性原理を表す)，下向きと上向きの二つの三角形が交わってできる六芒星の形(六角の星形で，現象世界を顕現させる力を表す)，五芒星(地･水･火･風･空の〈五大〉などを表す)などである。そのほかに〈門〉を表す形(聖域に入る入口を示す)，蓮の花弁の形(神格の属性としての願望を成就させる力などを表す)なども用いられる。…

※「直線」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」