レンズ空間（読み）レンズくうかん（英語表記）lens space

改訂新版　世界大百科事典

レンズ空間 (レンズくうかん)
lens space

Vを三次元球体，Sをその表面である二次元球面とし，大円Cで分かれるSの二つの半球面をE，E′とする。p，q（p＞0）を互いに素な整数として，Eの点xに対し，その点をCの軸のまわりに2πq/pだけ回転した点をつくり，さらにこの点のCの面に関する対称点をつくる。このとき得られるE′の点をφ（x）で表す。いま，Vにおいて，すべてのxについて，xとφ（x）をはり合わせた図形を考え，これをL（p，q）で表し，（p，q）型のレンズ空間という。これは次のようにも作れる。z₁＝x₁＋iy₁，z₂＝x₂＋iy₂を複素数とするとき，｜z₁｜²＋｜z₂｜²＝1はx₁²＋y₁²＋x₂²＋y₂²＝1と同値だから，｜z₁｜²＋｜z₂｜²＝1をみたす複素数の組（z₁，z₂）の全体は三次元球面S³を表す。このときに，同相写像h：S³→S³が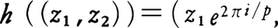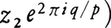で定義でき，g^p＝g◦……◦g（p個）は恒等写像となる。いま，S³において，すべての点x∈S³についてx，g（x），……，g^p⁻¹（x）を同一視したものがL（p，q）となる。L（p，q）は三次元の閉じた多様体で，とくにL（2，1）は三次元射影空間である。レンズ空間は興味ある多くの性質をもっている。
執筆者：中岡 稔

出典　株式会社平凡社「改訂新版　世界大百科事典」